| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 10 Straight Lines
Welcome to the solutions for Chapter 10: Straight Lines, a fundamental chapter in coordinate geometry that delves into the properties, equations, and relationships of lines within the Cartesian plane. Building upon the foundational concepts of coordinate systems and basic linear equations ($ax+by+c=0$), this chapter provides a comprehensive analytical framework for understanding straight lines. We move beyond simply plotting points to rigorously defining concepts like slope, exploring various standard forms for representing linear equations algebraically, and deriving formulas for calculating angles between lines, distances from points to lines, and distances between parallel lines. Mastering the techniques presented here is crucial for further studies in geometry, calculus (especially concerning tangents and normals), physics (kinematics, optics), and engineering.
The journey begins with a thorough revisit and formalization of the concept of the slope (or gradient) of a line, which quantifies its steepness or inclination. The slope, denoted by $m$, can be defined in two primary ways: trigonometrically as $m = \tan \theta$, where $\theta$ is the angle the line makes with the positive x-axis (its inclination), or algebraically using the coordinates of any two distinct points $(x_1, y_1)$ and $(x_2, y_2)$ on the line: $m = \frac{y_2 - y_1}{x_2 - x_1}$. Understanding slope is paramount as it leads directly to conditions for parallelism (two non-vertical lines are parallel if and only if their slopes are equal, $m_1 = m_2$) and perpendicularity (two non-vertical lines are perpendicular if and only if the product of their slopes is -1, $m_1m_2 = -1$). The solutions also derive and apply the formula for finding the acute angle $\phi$ between two intersecting lines with slopes $m_1$ and $m_2$: $\tan \phi = \left|\frac{m_1 - m_2}{1 + m_1m_2}\right|$, provided $1 + m_1m_2 \neq 0$.
A significant portion of this chapter is dedicated to mastering the various standard forms for the equation of a straight line. Each form is useful in different contexts, depending on the information given about the line. The solutions detail the derivation and application of these forms:
- Slope-Intercept form: $y = mx + c$, where $m$ is the slope and $c$ is the y-intercept.
- Point-Slope form: $y - y_1 = m(x - x_1)$, using the slope $m$ and a point $(x_1, y_1)$ on the line.
- Two-Point form: $\frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1}$, using two points $(x_1, y_1)$ and $(x_2, y_2)$ on the line.
- Intercept form: $\frac{x}{a} + \frac{y}{b} = 1$, where $a$ and $b$ are the x-intercept and y-intercept, respectively.
- Normal (or Perpendicular) form: $x \cos \omega + y \sin \omega = p$, where $p$ is the length of the perpendicular from the origin to the line, and $\omega$ is the angle this perpendicular makes with the positive x-axis.
Solutions demonstrate converting the general equation of a line, $Ax + By + C = 0$, into these various standard forms to extract information like slope or intercepts, and conversely, finding the equation of a line given specific geometric conditions (e.g., passing through two points, passing through a point and parallel/perpendicular to another line, having given intercepts).
Furthermore, crucial distance formulas are derived and applied. The formula for the perpendicular distance of a point $(x_1, y_1)$ from the line $Ax + By + C = 0$ is given by $d = \frac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}}$. This formula is fundamental. Using this, the method for calculating the distance between two parallel lines (e.g., $Ax + By + C_1 = 0$ and $Ax + By + C_2 = 0$) is also derived, often as $\frac{|C_1 - C_2|}{\sqrt{A^2 + B^2}}$. These formulas are applied in various problems, including finding coordinates related to geometric figures, such as the feet of perpendiculars drawn from a point to a line, the image of a point reflected across a line, or calculating properties related to triangles like centroids, incenters, circumcenters, and areas using coordinate methods involving straight lines. These comprehensive tools are essential for analytical geometry.
Example 1 to 5 (Before Exercise 10.1)
Example 1: Find the slope of the lines:
(a) Passing through the points (3, – 2) and (–1, 4),
(b) Passing through the points (3, – 2) and (7, – 2),
(c) Passing through the points (3, – 2) and (3, 4),
(d) Making inclination of 60° with the positive direction of x-axis.
Answer:
Given:
Various conditions defining lines.
To Find:
The slope of each given line.
Solution:
We use the following formulas for the slope of a line:
1. If a line passes through two points $(x_1, y_1)$ and $(x_2, y_2)$, its slope is $m = \frac{y_2 - y_1}{x_2 - x_1}$, provided $x_1 \neq x_2$.
2. If a line makes an inclination $\theta$ with the positive direction of the x-axis, its slope is $m = \tan \theta$, provided $\theta \neq 90^\circ$.
(a) Passing through the points (3, – 2) and (–1, 4)
Let $(x_1, y_1) = (3, -2)$ and $(x_2, y_2) = (-1, 4)$.
Using the formula $m = \frac{y_2 - y_1}{x_2 - x_1}$:
$m = \frac{4 - (-2)}{-1 - 3}$
$m = \frac{4 + 2}{-4}$
$m = \frac{6}{-4}$
$m = -\frac{3}{2}$
The slope of the line is $-\frac{3}{2}$.
(b) Passing through the points (3, – 2) and (7, – 2)
Let $(x_1, y_1) = (3, -2)$ and $(x_2, y_2) = (7, -2)$.
Using the formula $m = \frac{y_2 - y_1}{x_2 - x_1}$:
$m = \frac{-2 - (-2)}{7 - 3}$
$m = \frac{-2 + 2}{4}$
$m = \frac{0}{4}$
$m = 0$
The slope of the line is $0$. This indicates a horizontal line.
(c) Passing through the points (3, – 2) and (3, 4)
Let $(x_1, y_1) = (3, -2)$ and $(x_2, y_2) = (3, 4)$.
Using the formula $m = \frac{y_2 - y_1}{x_2 - x_1}$:
$m = \frac{4 - (-2)}{3 - 3}$
$m = \frac{4 + 2}{0}$
$m = \frac{6}{0}$
Division by zero is undefined.
The slope of the line is undefined. This indicates a vertical line.
(d) Making inclination of 60° with the positive direction of x-axis
The inclination is $\theta = 60^\circ$.
Using the formula $m = \tan \theta$:
$m = \tan 60^\circ$
We know that $\tan 60^\circ = \sqrt{3}$.
$m = \sqrt{3}$
The slope of the line is $\sqrt{3}$.
Example 2: If the angle between two lines is $\frac{π}{4}$ and slope of one of the lines is $\frac{1}{2}$, find the slope of the other line.
Answer:
Given:
Angle between two lines, $\theta = \frac{\pi}{4}$.
Slope of one line, $m_1 = \frac{1}{2}$.
To Find:
The slope of the other line (let's call it $m_2$).
Solution:
The formula for the angle $\theta$ between two lines with slopes $m_1$ and $m_2$ is given by:
$\tan \theta = \left|\frac{m_2 - m_1}{1 + m_1 m_2}\right|$
We are given $\theta = \frac{\pi}{4}$ and $m_1 = \frac{1}{2}$. We know that $\tan \frac{\pi}{4} = 1$.
Substitute the given values into the formula:
$1 = \left|\frac{m_2 - \frac{1}{2}}{1 + \frac{1}{2} m_2}\right|$
Simplify the expression inside the absolute value:
$1 = \left|\frac{\frac{2m_2 - 1}{2}}{\frac{2 + m_2}{2}}\right|$
$1 = \left|\frac{2m_2 - 1}{2 + m_2}\right|$
This equation implies two possible cases:
Case 1: $\frac{2m_2 - 1}{2 + m_2} = 1$
Assuming $2 + m_2 \neq 0$, multiply both sides by $(2 + m_2)$:
$2m_2 - 1 = 2 + m_2$
$2m_2 - m_2 = 2 + 1$
$m_2 = 3$
Check $1 + m_1 m_2 = 1 + \frac{1}{2}(3) = 1 + \frac{3}{2} = \frac{5}{2} \neq 0$. This solution is valid.
Case 2: $\frac{2m_2 - 1}{2 + m_2} = -1$
Assuming $2 + m_2 \neq 0$, multiply both sides by $(2 + m_2)$:
$2m_2 - 1 = -(2 + m_2)$
$2m_2 - 1 = -2 - m_2$
$2m_2 + m_2 = -2 + 1$
$3m_2 = -1$
$m_2 = -\frac{1}{3}$
Check $1 + m_1 m_2 = 1 + \frac{1}{2}(-\frac{1}{3}) = 1 - \frac{1}{6} = \frac{5}{6} \neq 0$. This solution is also valid.
Thus, there are two possible values for the slope of the other line.
The slope of the other line is $3$ or $-\frac{1}{3}$.
Example 3: Line through the points (–2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of x.
Answer:
Given:
Line 1 passes through points $(-2, 6)$ and $(4, 8)$.
Line 2 passes through points $(8, 12)$ and $(x, 24)$.
Line 1 is perpendicular to Line 2.
To Find:
The value of $x$.
Solution:
The slope of a line passing through two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the formula $m = \frac{y_2 - y_1}{x_2 - x_1}$ (provided $x_1 \neq x_2$).
Let $m_1$ be the slope of the line passing through $(-2, 6)$ and $(4, 8)$.
$m_1 = \frac{8 - 6}{4 - (-2)}$
$m_1 = \frac{2}{4 + 2}$
$m_1 = \frac{2}{6}$
$m_1 = \frac{1}{3}$
Let $m_2$ be the slope of the line passing through $(8, 12)$ and $(x, 24)$.
$m_2 = \frac{24 - 12}{x - 8}$
$m_2 = \frac{12}{x - 8}$
Given that the two lines are perpendicular, the product of their slopes is $-1$, provided neither line is vertical or horizontal.
Since $m_1 = \frac{1}{3}$ is a finite non-zero slope, neither line is vertical or horizontal. Thus, their slopes must satisfy the condition $m_1 m_2 = -1$.
$m_1 \times m_2 = -1$
(Condition for perpendicular lines)
Substitute the expressions for $m_1$ and $m_2$:
$\frac{1}{3} \times \frac{12}{x - 8} = -1$
$\frac{12}{3(x - 8)} = -1$
$\frac{4}{x - 8} = -1$
Assuming $x - 8 \neq 0$, multiply both sides by $(x - 8)$:
$4 = -1 \times (x - 8)$
$4 = -x + 8$
Add $x$ to both sides and subtract 4 from both sides:
$x = 8 - 4$
$x = 4$
The value $x=4$ ensures $x-8 = 4-8 = -4 \neq 0$, so the slope $m_2$ is defined.
The value of $x$ is 4.
Example 4: Three points P (h, k), Q (x1 , y1 ) and R (x2 , y2 ) lie on a line. Show that
(h – x1) (y2 – y1) = (k – y1) (x2 – x1).
Answer:
Given:
Three points P$(h, k)$, Q$(x_1, y_1)$, and R$(x_2, y_2)$ lie on a line (are collinear).
To Show:
$(h - x_1) (y_2 - y_1) = (k - y_1) (x_2 - x_1)$.
Proof:
Since the points P, Q, and R are collinear, the slope of the line segment PQ must be equal to the slope of the line segment QR (provided the slopes are defined).
The slope of the line passing through two points $(x_a, y_a)$ and $(x_b, y_b)$ is given by $m = \frac{y_b - y_a}{x_b - x_a}$, provided $x_a \neq x_b$.
Slope of PQ ($m_{PQ}$) using points P$(h, k)$ and Q$(x_1, y_1)$:
$m_{PQ} = \frac{k - y_1}{h - x_1}$ (assuming $h \neq x_1$)
Slope of QR ($m_{QR}$) using points Q$(x_1, y_1)$ and R$(x_2, y_2)$:
$m_{QR} = \frac{y_2 - y_1}{x_2 - x_1}$ (assuming $x_1 \neq x_2$)
Since P, Q, R are collinear, $m_{PQ} = m_{QR}$ (if the line is not vertical).
$\frac{k - y_1}{h - x_1} = \frac{y_2 - y_1}{x_2 - x_1}$
Cross-multiply the terms (assuming $h \neq x_1$ and $x_2 \neq x_1$):
$(k - y_1)(x_2 - x_1) = (h - x_1)(y_2 - y_1)$
This is the required equation, just with sides swapped:
$(h - x_1)(y_2 - y_1) = (k - y_1)(x_2 - x_1)$
Consider the special cases:
Case 1: Vertical line
If the three points lie on a vertical line, their x-coordinates are the same. Thus, $h = x_1 = x_2$.
In this case, $h - x_1 = 0$ and $x_2 - x_1 = 0$.
The equation to be shown becomes $(0)(y_2 - y_1) = (k - y_1)(0)$, which simplifies to $0 = 0$. This is true.
Case 2: Horizontal line
If the three points lie on a horizontal line, their y-coordinates are the same. Thus, $k = y_1 = y_2$.
In this case, $k - y_1 = 0$ and $y_2 - y_1 = 0$.
The equation to be shown becomes $(h - x_1)(0) = (0)(x_2 - x_1)$, which simplifies to $0 = 0$. This is true.
In all cases (non-vertical, non-horizontal, vertical, or horizontal), the relationship $(h - x_1)(y_2 - y_1) = (k - y_1)(x_2 - x_1)$ holds true if the points P, Q, and R are collinear.
Hence, shown.
Example 5: In Fig 10.9, time and distance graph of a linear motion is given. Two positions of time and distance are recorded as, when T = 0, D = 2 and when T = 3, D = 8. Using the concept of slope, find law of motion, i.e., how distance depends upon time.
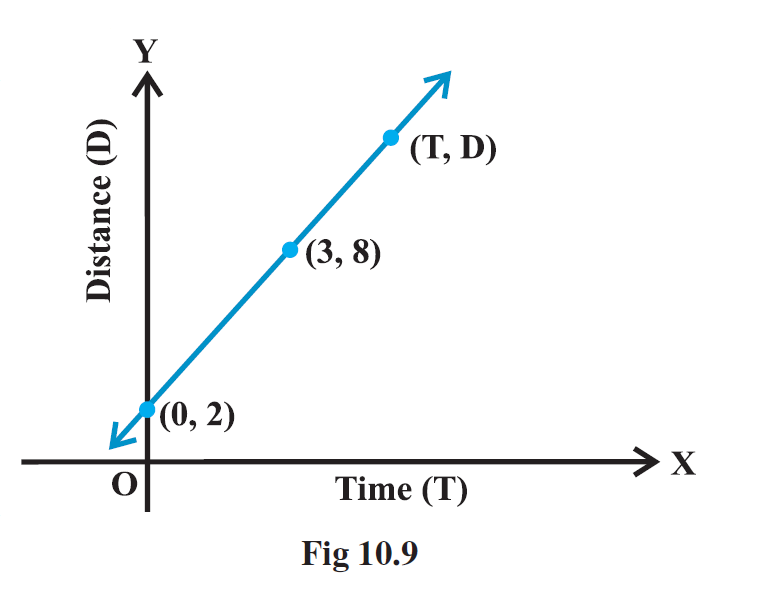
Answer:
Given:
The time and distance graph of a linear motion passes through two points recorded as:
When $T = 0$, $D = 2$. This corresponds to the point $(T_1, D_1) = (0, 2)$.
When $T = 3$, $D = 8$. This corresponds to the point $(T_2, D_2) = (3, 8)$.
To Find:
The law of motion, which describes how distance (D) depends upon time (T), using the concept of slope.
Solution:
Since the time and distance graph represents a linear motion, it is a straight line. The relationship between distance (D) and time (T) can be expressed in the form of a linear equation: $D = mT + c$, where $m$ is the slope of the line and $c$ is the D-intercept (the value of D when $T=0$).
The slope ($m$) of the line passing through two points $(T_1, D_1)$ and $(T_2, D_2)$ is given by the formula:
$m = \frac{D_2 - D_1}{T_2 - T_1}$
Using the given points $(0, 2)$ and $(3, 8)$:
$m = \frac{8 - 2}{3 - 0}$
$m = \frac{6}{3}$
$m = 2$
The D-intercept ($c$) is the value of D when $T = 0$. From the given information, when $T = 0$, $D = 2$.
$c = 2$
Substitute the values of the slope ($m=2$) and the D-intercept ($c=2$) into the linear equation $D = mT + c$:
$D = 2T + 2$
This equation represents the law of motion, showing how the distance D depends on time T.
The law of motion is $D = 2T + 2$.
Exercise 10.1
Question 1. Draw a quadrilateral in the Cartesian plane, whose vertices are (– 4, 5), (0, 7), (5, – 5) and (– 4, –2). Also, find its area.
Answer:
Given:
The vertices of the quadrilateral are A$(-4, 5)$, B$(0, 7)$, C$(5, -5)$, and D$(-4, -2)$.
To Find:
1. Draw the quadrilateral in the Cartesian plane.
2. Find the area of the quadrilateral.
Solution:
To draw the quadrilateral, we plot the given points A$(-4, 5)$, B$(0, 7)$, C$(5, -5)$, and D$(-4, -2)$ on a Cartesian plane and join them in order. Since vertex A and vertex D have the same x-coordinate $(-4)$, the side AD is a vertical line segment. (Drawing cannot be shown in this text format).
To find the area of the quadrilateral ABCD, we can divide it into two triangles by joining two non-adjacent vertices, for example, A and C. The area of the quadrilateral will be the sum of the areas of $\triangle ABC$ and $\triangle ADC$.
The formula for the area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Area of $\triangle ABC$:
Vertices are A$(-4, 5)$, B$(0, 7)$, C$(5, -5)$.
$(x_1, y_1) = (-4, 5)$, $(x_2, y_2) = (0, 7)$, $(x_3, y_3) = (5, -5)$
Area$(\triangle ABC) = \frac{1}{2} |(-4)(7 - (-5)) + (0)(-5 - 5) + (5)(5 - 7)|$
Area$(\triangle ABC) = \frac{1}{2} |(-4)(12) + (0)(-10) + (5)(-2)|$
Area$(\triangle ABC) = \frac{1}{2} |-48 + 0 - 10|$
Area$(\triangle ABC) = \frac{1}{2} |-58|$
Area$(\triangle ABC) = \frac{1}{2} \times 58 = 29$ square units.
Area of $\triangle ADC$:
Vertices are A$(-4, 5)$, D$(-4, -2)$, C$(5, -5)$.
$(x_1, y_1) = (-4, 5)$, $(x_2, y_2) = (-4, -2)$, $(x_3, y_3) = (5, -5)$
Area$(\triangle ADC) = \frac{1}{2} |(-4)(-2 - (-5)) + (-4)(-5 - 5) + (5)(5 - (-2))|$
Area$(\triangle ADC) = \frac{1}{2} |(-4)(-2 + 5) + (-4)(-10) + (5)(5 + 2)|$
Area$(\triangle ADC) = \frac{1}{2} |(-4)(3) + 40 + (5)(7)|$
Area$(\triangle ADC) = \frac{1}{2} |-12 + 40 + 35|$
Area$(\triangle ADC) = \frac{1}{2} |63|$
Area$(\triangle ADC) = \frac{1}{2} \times 63 = 31.5$ square units.
The area of the quadrilateral ABCD is the sum of the areas of $\triangle ABC$ and $\triangle ADC$.
Area(ABCD) = Area$(\triangle ABC)$ + Area$(\triangle ADC)$
Area(ABCD) = $29 + 31.5 = 60.5$ square units.
Question 2. The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.
Answer:
Given:
An equilateral triangle with side length $2a$.
The base of the triangle lies along the y-axis.
The mid-point of the base is at the origin $(0, 0)$.
To Find:
The coordinates of the vertices of the triangle.
Solution:
Let the base of the equilateral triangle be BC.
The length of the base is $BC = 2a$.
The base lies along the y-axis, and its mid-point is at the origin (0, 0).
Since the mid-point of BC is the origin, the distance from the origin to B is equal to the distance from the origin to C, and this distance is half the length of the base, i.e., $\frac{2a}{2} = a$.
Since B and C lie on the y-axis and their mid-point is the origin, their coordinates must be of the form $(0, y)$.
Let the coordinates of B be $(0, -a)$ and the coordinates of C be $(0, a)$.
The distance between B and C is $\sqrt{(0-0)^2 + (a - (-a))^2} = \sqrt{0^2 + (2a)^2} = \sqrt{4a^2} = 2a$, which matches the given side length.
Let the third vertex be A$(x, y)$. Since it's an equilateral triangle, the distance from A to B must be equal to the distance from A to C, and also equal to the side length $2a$.
$AB = AC = BC = 2a$.
Since the base BC lies on the y-axis and its mid-point is the origin, the third vertex A must lie on the x-axis (or on the line $y=0$) if the triangle is oriented symmetrically with respect to the y-axis. The perpendicular bisector of BC is the x-axis.
Let the coordinates of A be $(x, 0)$.
Now, use the distance formula for AB and AC. We'll use $AB = 2a$ or $AC = 2a$. Let's use AC.
$AC^2 = (x_A - x_C)^2 + (y_A - y_C)^2$
$(2a)^2 = (x - 0)^2 + (0 - a)^2$
$4a^2 = x^2 + (-a)^2$
$4a^2 = x^2 + a^2$
$x^2 = 4a^2 - a^2$
$x^2 = 3a^2$
$x = \pm \sqrt{3a^2} = \pm \sqrt{3}a$
So, the x-coordinate of the third vertex A can be $\sqrt{3}a$ or $-\sqrt{3}a$. The y-coordinate is 0 because it lies on the perpendicular bisector of the base (the x-axis).
The vertices of the triangle are:
Vertex B: $(0, -a)$
Vertex C: $(0, a)$
Vertex A: $(\sqrt{3}a, 0)$ or $(-\sqrt{3}a, 0)$
There are two possible locations for the third vertex, one on the positive x-axis side and one on the negative x-axis side.
The vertices of the triangle are $(0, -a)$, $(0, a)$, and $(\sqrt{3}a, 0)$ or $(0, -a)$, $(0, a)$, and $(-\sqrt{3}a, 0)$.
Question 3. Find the distance between P (x1 , y1 ) and Q (x2 , y2 ) when:
(i) PQ is parallel to the y-axis,
(ii) PQ is parallel to the x-axis.
Answer:
Given:
Two points P$(x_1, y_1)$ and Q$(x_2, y_2)$.
To Find:
The distance between P and Q under the given conditions.
Solution:
The distance between two points P$(x_1, y_1)$ and Q$(x_2, y_2)$ is given by the distance formula:
$PQ = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
(i) PQ is parallel to the y-axis
If the line segment PQ is parallel to the y-axis, it means that the x-coordinates of the points P and Q are the same.
So, $x_1 = x_2$.
Substitute $x_2 = x_1$ into the distance formula:
$PQ = \sqrt{(x_1 - x_1)^2 + (y_2 - y_1)^2}$
$PQ = \sqrt{(0)^2 + (y_2 - y_1)^2}$
$PQ = \sqrt{(y_2 - y_1)^2}$
$PQ = |y_2 - y_1|$
The distance is the absolute difference between the y-coordinates.
(ii) PQ is parallel to the x-axis
If the line segment PQ is parallel to the x-axis, it means that the y-coordinates of the points P and Q are the same.
So, $y_1 = y_2$.
Substitute $y_2 = y_1$ into the distance formula:
$PQ = \sqrt{(x_2 - x_1)^2 + (y_1 - y_1)^2}$
$PQ = \sqrt{(x_2 - x_1)^2 + (0)^2}$
$PQ = \sqrt{(x_2 - x_1)^2}$
$PQ = |x_2 - x_1|$
The distance is the absolute difference between the x-coordinates.
Question 4. Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
Answer:
Given:
Two points A$(7, 6)$ and B$(3, 4)$.
To Find:
A point on the x-axis which is equidistant from A and B.
Solution:
A point on the x-axis has its y-coordinate equal to 0.
Let the required point on the x-axis be P$(x, 0)$.
Since P is equidistant from points A$(7, 6)$ and B$(3, 4)$, the distance PA must be equal to the distance PB.
$PA = PB$
Squaring both sides, we get $PA^2 = PB^2$.
Using the distance formula, the square of the distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is $(x_2 - x_1)^2 + (y_2 - y_1)^2$.
Calculate $PA^2$ using points P$(x, 0)$ and A$(7, 6)$:
$PA^2 = (x - 7)^2 + (0 - 6)^2$
$PA^2 = (x - 7)^2 + (-6)^2$
$PA^2 = (x - 7)^2 + 36$
Calculate $PB^2$ using points P$(x, 0)$ and B$(3, 4)$:
$PB^2 = (x - 3)^2 + (0 - 4)^2$
$PB^2 = (x - 3)^2 + (-4)^2$
$PB^2 = (x - 3)^2 + 16$
Set $PA^2 = PB^2$:
$(x - 7)^2 + 36 = (x - 3)^2 + 16$
Expand the squared terms using $(a-b)^2 = a^2 - 2ab + b^2$:
$(x^2 - 14x + 49) + 36 = (x^2 - 6x + 9) + 16$
$x^2 - 14x + 85 = x^2 - 6x + 25$
Subtract $x^2$ from both sides:
$-14x + 85 = -6x + 25$
Rearrange the terms to solve for $x$. Add $14x$ to both sides and subtract 25 from both sides:
$85 - 25 = -6x + 14x$
$60 = 8x$
$x = \frac{60}{8}$
$x = \frac{\cancel{60}^{15}}{\cancel{8}_{2}} = \frac{15}{2}$
The x-coordinate of the point is $\frac{15}{2}$. Since the point is on the x-axis, its y-coordinate is 0.
The required point is $\left(\frac{15}{2}, 0\right)$.
Question 5. Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, – 4) and B (8, 0).
Answer:
Given:
The line passes through the origin O$(0, 0)$.
The line also passes through the mid-point of the line segment joining points P$(0, -4)$ and B$(8, 0)$.
To Find:
The slope of the line.
Solution:
First, let's find the coordinates of the mid-point of the line segment joining P$(0, -4)$ and B$(8, 0)$.
The mid-point M of a line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is given by the formula $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Using points P$(0, -4)$ and B$(8, 0)$, the coordinates of the mid-point M are:
$M = \left(\frac{0 + 8}{2}, \frac{-4 + 0}{2}\right)$
$M = \left(\frac{8}{2}, \frac{-4}{2}\right)$
$M = (4, -2)$
The line passes through the origin O$(0, 0)$ and the mid-point M$(4, -2)$.
Now, we find the slope of the line passing through these two points.
The slope ($m$) of a line passing through two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m = \frac{y_2 - y_1}{x_2 - x_1}$, provided $x_1 \neq x_2$.
Using points O$(0, 0)$ and M$(4, -2)$:
$(x_1, y_1) = (0, 0)$
$(x_2, y_2) = (4, -2)$
$m = \frac{-2 - 0}{4 - 0}$
$m = \frac{-2}{4}$
$m = -\frac{1}{2}$
The slope of the line is $-\frac{1}{2}$.
Question 6. Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.
Answer:
Given:
The three points are A$(4, 4)$, B$(3, 5)$, and C$(-1, -1)$.
To Show:
The points A, B, and C are the vertices of a right-angled triangle, without using the Pythagoras theorem.
Solution:
To show that the points form a right-angled triangle without using the Pythagoras theorem, we can use the concept of slopes. If two sides of a triangle are perpendicular, then the angle between them is $90^\circ$, and the triangle is right-angled.
Two lines with slopes $m_1$ and $m_2$ are perpendicular if the product of their slopes is $-1$, i.e., $m_1 m_2 = -1$ (provided neither line is vertical or horizontal).
Let's calculate the slopes of the line segments AB, BC, and AC.
The slope of a line passing through points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m = \frac{y_2 - y_1}{x_2 - x_1}$ (for $x_1 \neq x_2$).
Slope of AB ($m_{AB}$) using A$(4, 4)$ and B$(3, 5)$:
$m_{AB} = \frac{5 - 4}{3 - 4} = \frac{1}{-1} = -1$
Slope of BC ($m_{BC}$) using B$(3, 5)$ and C$(-1, -1)$:
$m_{BC} = \frac{-1 - 5}{-1 - 3} = \frac{-6}{-4} = \frac{3}{2}$
Slope of AC ($m_{AC}$) using A$(4, 4)$ and C$(-1, -1)$:
$m_{AC} = \frac{-1 - 4}{-1 - 4} = \frac{-5}{-5} = 1$
Now, let's check the product of the slopes of pairs of sides:
$m_{AB} \times m_{BC} = (-1) \times \frac{3}{2} = -\frac{3}{2}$
$m_{BC} \times m_{AC} = \frac{3}{2} \times 1 = \frac{3}{2}$
$m_{AB} \times m_{AC} = (-1) \times 1 = -1$
Since $m_{AB} \times m_{AC} = -1$, the line segment AB is perpendicular to the line segment AC.
This means that the angle between sides AB and AC is $90^\circ$, which is the angle at vertex A.
Therefore, the triangle ABC is a right-angled triangle with the right angle at vertex A.
Hence, shown.
Question 7. Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
Answer:
Given:
The line makes an angle of 30° with the positive direction of the y-axis, measured anticlockwise.
To Find:
The slope of the line.
Solution:
The slope of a line is defined as the tangent of the angle it makes with the positive direction of the x-axis, measured anticlockwise. This angle is called the inclination of the line, denoted by $\theta$. The slope is $m = \tan \theta$.
The given angle is the angle made with the positive y-axis. Let's find the angle made with the positive x-axis (the inclination $\theta$).
Consider the angles from the positive x-axis (horizontal) and the positive y-axis (vertical), measured anticlockwise from their respective positive directions.
The positive y-axis is at an angle of $90^\circ$ ($\frac{\pi}{2}$ radians) from the positive x-axis, measured anticlockwise.
The line makes an angle of 30° with the positive y-axis, measured anticlockwise from the positive y-axis.
Starting from the positive x-axis and moving anticlockwise:
We first reach the positive y-axis at $90^\circ$.
From the positive y-axis, the line is at an additional angle of 30° (measured anticlockwise).
So, the total angle from the positive x-axis to the line, measured anticlockwise (the inclination $\theta$), is the sum of the angle to the positive y-axis and the angle from the positive y-axis to the line.
$\theta = 90^\circ + 30^\circ = 120^\circ$.
Now, find the slope using the inclination $\theta = 120^\circ$:
$m = \tan \theta = \tan 120^\circ$
We know that $\tan (180^\circ - \alpha) = -\tan \alpha$.
$\tan 120^\circ = \tan (180^\circ - 60^\circ) = -\tan 60^\circ$
We know that $\tan 60^\circ = \sqrt{3}$.
$m = -\sqrt{3}$
The slope of the line is $-\sqrt{3}$.
Question 8. Find the value of x for which the points (x, – 1), (2,1) and (4, 5) are collinear.
Answer:
Given:
The three points are $A(x, -1)$, $B(2, 1)$, and $C(4, 5)$.
To Find:
The value of $x$ for which the points are collinear.
Solution:
For three points to be collinear, the slope between any two pairs of points must be equal.
Let the points be $A(x_1, y_1)$, $B(x_2, y_2)$, and $C(x_3, y_3)$.
Here, $x_1 = x$, $y_1 = -1$, $x_2 = 2$, $y_2 = 1$, $x_3 = 4$, $y_3 = 5$.
Slope of the line segment AB is given by $m_{AB} = \frac{y_2 - y_1}{x_2 - x_1}$.
$m_{AB} = \frac{1 - (-1)}{2 - x} = \frac{1 + 1}{2 - x} = \frac{2}{2 - x}$
Slope of the line segment BC is given by $m_{BC} = \frac{y_3 - y_2}{x_3 - x_2}$.
$m_{BC} = \frac{5 - 1}{4 - 2} = \frac{4}{2} = 2$
For the points A, B, and C to be collinear, the slope of AB must be equal to the slope of BC.
$m_{AB} = m_{BC}$
$\frac{2}{2 - x} = 2$
Multiply both sides by $(2 - x)$, assuming $x \neq 2$ (If $x=2$, point A becomes (2, -1), which is not collinear with (2,1) and (4,5) as they form a vertical line through $x=2$).
$2 = 2(2 - x)$
Divide both sides by 2.
$1 = 2 - x$
Add $x$ to both sides.
$x + 1 = 2$
Subtract 1 from both sides.
$x = 2 - 1$
$x = 1$
The value of $x$ for which the points $(x, – 1)$, $(2,1)$ and $(4, 5)$ are collinear is 1.
Question 9. Without using distance formula, show that points (– 2, – 1), (4, 0), (3, 3) and (–3, 2) are the vertices of a parallelogram.
Answer:
Given:
The four points are $A(-2, -1)$, $B(4, 0)$, $C(3, 3)$, and $D(-3, 2)$.
To Show:
The points $A$, $B$, $C$, and $D$ are the vertices of a parallelogram.
Proof:
A quadrilateral is a parallelogram if its opposite sides are parallel. We can show that the opposite sides are parallel by comparing their slopes. The slope of a line segment joining points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m = \frac{y_2 - y_1}{x_2 - x_1}$.
Let's calculate the slopes of the four sides of the quadrilateral ABCD:
Slope of AB ($m_{AB}$): Points A$(-2, -1)$ and B$(4, 0)$.
$m_{AB} = \frac{0 - (-1)}{4 - (-2)} = \frac{0 + 1}{4 + 2} = \frac{1}{6}$
Slope of BC ($m_{BC}$): Points B$(4, 0)$ and C$(3, 3)$.
$m_{BC} = \frac{3 - 0}{3 - 4} = \frac{3}{-1} = -3$
Slope of CD ($m_{CD}$): Points C$(3, 3)$ and D$(-3, 2)$.
$m_{CD} = \frac{2 - 3}{-3 - 3} = \frac{-1}{-6} = \frac{1}{6}$
Slope of DA ($m_{DA}$): Points D$(-3, 2)$ and A$(-2, -1)$.
$m_{DA} = \frac{-1 - 2}{-2 - (-3)} = \frac{-3}{-2 + 3} = \frac{-3}{1} = -3$
Now, we compare the slopes of the opposite sides:
We observe that $m_{AB} = \frac{1}{6}$ and $m_{CD} = \frac{1}{6}$.
Since $m_{AB} = m_{CD}$, the line segment AB is parallel to the line segment CD.
We also observe that $m_{BC} = -3$ and $m_{DA} = -3$.
Since $m_{BC} = m_{DA}$, the line segment BC is parallel to the line segment DA.
Since both pairs of opposite sides (AB and CD, and BC and DA) are parallel, the quadrilateral ABCD is a parallelogram.
Alternatively, we could use the property that the diagonals of a parallelogram bisect each other, meaning their midpoints coincide. The midpoint of a segment joining $(x_1, y_1)$ and $(x_2, y_2)$ is $\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)$.
Midpoint of diagonal AC: Points A$(-2, -1)$ and C$(3, 3)$.
Midpoint$_{AC} = \left(\frac{-2 + 3}{2}, \frac{-1 + 3}{2}\right) = \left(\frac{1}{2}, \frac{2}{2}\right) = \left(\frac{1}{2}, 1\right)$
Midpoint of diagonal BD: Points B$(4, 0)$ and D$(-3, 2)$.
Midpoint$_{BD} = \left(\frac{4 + (-3)}{2}, \frac{0 + 2}{2}\right) = \left(\frac{1}{2}, \frac{2}{2}\right) = \left(\frac{1}{2}, 1\right)$
Since Midpoint$_{AC}$ = Midpoint$_{BD}$, the diagonals AC and BD bisect each other. Therefore, the quadrilateral ABCD is a parallelogram.
Question 10. Find the angle between the x-axis and the line joining the points (3, –1) and (4, –2).
Answer:
Given:
The two points are $A(3, -1)$ and $B(4, -2)$.
To Find:
The angle between the x-axis and the line joining the points $A$ and $B$.
Solution:
Let the line joining the points $(x_1, y_1)$ and $(x_2, y_2)$ make an angle $\theta$ with the positive x-axis. The slope ($m$) of the line is given by the formula:
$m = \frac{y_2 - y_1}{x_2 - x_1}$
Here, $(x_1, y_1) = (3, -1)$ and $(x_2, y_2) = (4, -2)$.
The slope of the line joining points $A$ and $B$ is:
$m = \frac{-2 - (-1)}{4 - 3}$
$m = \frac{-2 + 1}{1}$
$m = \frac{-1}{1}$
$m = -1$
The slope of a line is also equal to the tangent of the angle $\theta$ it makes with the positive x-axis:
$m = \tan \theta$
So, we have:
$\tan \theta = -1$
The angle $\theta$ whose tangent is $-1$ is $135^\circ$ (or $\frac{3\pi}{4}$ radians).
This angle is measured counter-clockwise from the positive x-axis to the line.
$\theta = \tan^{-1}(-1) = 135^\circ$
The angle between the x-axis and the line joining the given points is $135^\circ$.
Question 11. The slope of a line is double of the slope of another line. If tangent of the angle between them is $\frac{1}{3}$, find the slopes of the lines.
Answer:
Given:
Let the slopes of the two lines be $m_1$ and $m_2$.
One slope is double the other. Let's assume $m_1 = 2m_2$.
The tangent of the angle between the lines is $\frac{1}{3}$.
To Find:
The values of the slopes $m_1$ and $m_2$.
Solution:
The formula for the tangent of the angle $\theta$ between two lines with slopes $m_1$ and $m_2$ is given by:
$\tan \theta = \left|\frac{m_1 - m_2}{1 + m_1 m_2}\right|$
We are given that $\tan \theta = \frac{1}{3}$. Substituting this and $m_1 = 2m_2$ into the formula:
$\frac{1}{3} = \left|\frac{2m_2 - m_2}{1 + (2m_2) m_2}\right|$
$\frac{1}{3} = \left|\frac{m_2}{1 + 2m_2^2}\right|$
Since $1 + 2m_2^2$ is always positive for any real value of $m_2$, we can write:
$\frac{1}{3} = \frac{|m_2|}{1 + 2m_2^2}$
This gives us $1 + 2m_2^2 = 3|m_2|$.
We need to consider two cases based on the sign of $m_2$:
Case 1: $m_2 \geq 0$
In this case, $|m_2| = m_2$. The equation becomes:
$1 + 2m_2^2 = 3m_2$
$2m_2^2 - 3m_2 + 1 = 0$
This is a quadratic equation in $m_2$. We can factor it:
$(2m_2 - 1)(m_2 - 1) = 0$
This gives two possible values for $m_2$:
$2m_2 - 1 = 0 \implies m_2 = \frac{1}{2}$
$m_2 - 1 = 0 \implies m_2 = 1$
If $m_2 = \frac{1}{2}$, then $m_1 = 2m_2 = 2 \times \frac{1}{2} = 1$. The slopes are $\frac{1}{2}$ and $1$.
If $m_2 = 1$, then $m_1 = 2m_2 = 2 \times 1 = 2$. The slopes are $1$ and $2$.
Case 2: $m_2 < 0$
In this case, $|m_2| = -m_2$. The equation becomes:
$1 + 2m_2^2 = 3(-m_2)$
$1 + 2m_2^2 = -3m_2$
$2m_2^2 + 3m_2 + 1 = 0$
This is another quadratic equation in $m_2$. We can factor it:
$(2m_2 + 1)(m_2 + 1) = 0$
This gives two possible values for $m_2$:
$2m_2 + 1 = 0 \implies m_2 = -\frac{1}{2}$
$m_2 + 1 = 0 \implies m_2 = -1$
If $m_2 = -\frac{1}{2}$, then $m_1 = 2m_2 = 2 \times (-\frac{1}{2}) = -1$. The slopes are $-\frac{1}{2}$ and $-1$.
If $m_2 = -1$, then $m_1 = 2m_2 = 2 \times (-1) = -2$. The slopes are $-1$ and $-2$.
If we had initially assumed $m_2 = 2m_1$, the process would be symmetric, leading to the same sets of slopes.
Thus, there are four possible pairs of slopes for the two lines.
The possible pairs of slopes for the two lines are $(1, 2)$, $(\frac{1}{2}, 1)$, $(-1, -2)$, and $(-\frac{1}{2}, -1)$.
Question 12. A line passes through (x1 , y1 ) and (h, k). If slope of the line is m, show that
k – y1 = m (h – x1).
Answer:
Given:
A line passes through the points $(x_1, y_1)$ and $(h, k)$.
The slope of the line is $m$.
To Show:
$k - y_1 = m(h - x_1)$
Proof:
The slope of a line passing through two points $(x_a, y_a)$ and $(x_b, y_b)$ is defined as the ratio of the change in the y-coordinates to the change in the x-coordinates. The formula for the slope ($m$) is:
$m = \frac{y_b - y_a}{x_b - x_a}$
In this problem, the two points are $(x_1, y_1)$ and $(h, k)$. We can consider $(x_a, y_a) = (x_1, y_1)$ and $(x_b, y_b) = (h, k)$.
Using the slope formula with the given points, we have:
$m = \frac{k - y_1}{h - x_1}$
To obtain the desired expression, we can multiply both sides of the equation by the denominator $(h - x_1)$, assuming $h \neq x_1$ (if $h = x_1$, the line is vertical, and its slope is undefined unless $k=y_1$, in which case the points are the same and the line is not uniquely defined. If $k \neq y_1$ and $h=x_1$, the slope is infinite, and the given equation would not hold in the standard form). For a finite slope $m$, we must have $h \neq x_1$.
Multiplying both sides by $(h - x_1)$:
$m \times (h - x_1) = \frac{k - y_1}{h - x_1} \times (h - x_1)$
This simplifies to:
$m(h - x_1) = k - y_1$
Rearranging the terms, we get:
$k - y_1 = m(h - x_1)$
This shows that the given relationship holds true based on the definition of the slope of a line passing through two points.
Question 13. If three points (h, 0), (a, b) and (0, k) lie on a line, show that $\frac{a}{h}$ + $\frac{b}{k}$ = 1.
Answer:
Given:
Three points $(h, 0)$, $(a, b)$, and $(0, k)$ are collinear.
To Show:
$\frac{a}{h} + \frac{b}{k} = 1$
Proof:
Since the three points are collinear, the slope between any two pairs of points must be equal.
Let the points be $A(h, 0)$, $B(a, b)$, and $C(0, k)$.
The slope of the line segment joining two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by $m = \frac{y_2 - y_1}{x_2 - x_1}$.
Slope of AB ($m_{AB}$): Points A$(h, 0)$ and B$(a, b)$.
$m_{AB} = \frac{b - 0}{a - h} = \frac{b}{a - h}$
Slope of BC ($m_{BC}$): Points B$(a, b)$ and C$(0, k)$.
$m_{BC} = \frac{k - b}{0 - a} = \frac{k - b}{-a} = \frac{b - k}{a}$
Since the points A, B, and C are collinear, the slope of AB must be equal to the slope of BC (assuming $a \neq h$ and $a \neq 0$. If $a=0$, then $B$ is $(0,b)$ and $C$ is $(0,k)$, both on the y-axis. For the points to be collinear, $A(h,0)$ must also be on the y-axis, meaning $h=0$. But the points are $(h,0)$ and $(0,k)$, so if $h=0$ and $a=0$, the points are $(0,0)$, $(0,b)$, $(0,k)$. If $h \neq 0$ and $k \neq 0$, then $a$ and $h$ cannot be zero simultaneously). Let's assume $h \neq 0$, $k \neq 0$, $a \neq h$, and $a \neq 0$ for the slopes to be well-defined initially.
$m_{AB} = m_{BC}$
$\frac{b}{a - h} = \frac{b - k}{a}$
Cross-multiply the terms:
$b \times a = (b - k) \times (a - h)$
$ab = ba - bh - ka + kh$
Subtract $ab$ from both sides:
$0 = -bh - ka + kh$
Move the negative terms to the other side:
$bh + ka = kh$
Assuming $h \neq 0$ and $k \neq 0$, we can divide the entire equation by $kh$:
$\frac{bh}{kh} + \frac{ka}{kh} = \frac{kh}{kh}$
Cancel out common terms in each fraction:
$\frac{\cancel{h}b}{k\cancel{h}} + \frac{\cancel{k}a}{h\cancel{k}} = 1$
$\frac{b}{k} + \frac{a}{h} = 1$
Rearranging the terms, we get the desired result:
$\frac{a}{h} + \frac{b}{k} = 1$
This proves that if the three points $(h, 0)$, $(a, b)$, and $(0, k)$ are collinear, then $\frac{a}{h} + \frac{b}{k} = 1$, provided $h \neq 0$ and $k \neq 0$. If $h=0$ or $k=0$, the points would lie on the axes, and the equation $\frac{a}{h} + \frac{b}{k} = 1$ is interpreted as the intercept form of the line equation. The points $(h,0)$ and $(0,k)$ are the x and y intercepts respectively, assuming the line does not pass through the origin. If the line passes through the origin (i.e., $a=0$ and $b=0$), then point B is $(0,0)$. For $(h,0)$, $(0,0)$, and $(0,k)$ to be collinear, either $h=0$ (all on y-axis) or $k=0$ (all on x-axis) or they must coincide. If $h \neq 0, k \neq 0$, and the line passes through $(0,0)$, then $a=0, b=0$. In this case, $\frac{0}{h} + \frac{0}{k} = 0 \neq 1$, unless the line is the origin itself (points coincide), which doesn't form a line. Thus, the equation $\frac{a}{h} + \frac{b}{k} = 1$ specifically represents the case where the line has non-zero intercepts $h$ and $k$ on the x and y axes respectively.
Question 14. Consider the following population and year graph (Fig 10.10), find the slope of the line AB and using it, find what will be the population in the year 2010?
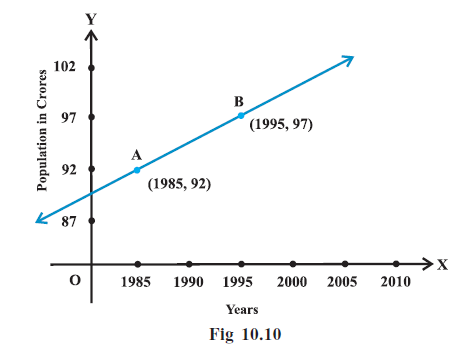
Answer:
Given:
From the graph, the line AB passes through two points representing (Year, Population).
Point A corresponds to the year 1985 and population 92 crores. So, point A is $(1985, 92)$.
Point B corresponds to the year 1995 and population 97 crores. So, point B is $(1995, 97)$.
To Find:
1. The slope of the line AB.
2. The population in the year 2010 using the slope.
Solution:
Let the points be $(x_1, y_1)$ and $(x_2, y_2)$, where the x-coordinate represents the year and the y-coordinate represents the population in crores.
Here, $(x_1, y_1) = (1985, 92)$ and $(x_2, y_2) = (1995, 97)$.
1. Slope of the line AB:
The slope ($m$) of a line passing through points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the formula:
$m = \frac{y_2 - y_1}{x_2 - x_1}$
Substitute the coordinates of points A and B into the formula:
$m = \frac{97 - 92}{1995 - 1985}$
$m = \frac{5}{10}$
$m = \frac{1}{2}$
The slope of the line AB is $\frac{1}{2}$. This means that for every 2-year increase, the population increases by 1 crore.
2. Population in the year 2010:
We can use the point-slope form of the equation of a line, which is $y - y_1 = m(x - x_1)$, where $(x_1, y_1)$ is a point on the line and $m$ is the slope.
Using point A $(1985, 92)$ and the slope $m = \frac{1}{2}$:
$y - 92 = \frac{1}{2}(x - 1985)$
We want to find the population ($y$) when the year ($x$) is 2010. Substitute $x = 2010$ into the equation:
$y - 92 = \frac{1}{2}(2010 - 1985)$
$y - 92 = \frac{1}{2}(25)$
$y - 92 = 12.5$
$y = 92 + 12.5$
$y = 104.5$
The population is measured in crores.
The slope of the line AB is $\frac{1}{2}$.
The population in the year 2010 will be 104.5 crores.
Example 6 to 12 (Before Exercise 10.2)
Example 6: Find the equations of the lines parallel to axes and passing through (– 2, 3).
Answer:
Given:
A line passes through the point $(-2, 3)$.
To Find:
The equations of the lines passing through $(-2, 3)$ and parallel to the x-axis and y-axis.
Solution:
We need to find the equations of two lines:
1. A line parallel to the x-axis and passing through $(-2, 3)$.
2. A line parallel to the y-axis and passing through $(-2, 3)$.
A line parallel to the x-axis has the form $y = c$, where $c$ is a constant. Since the line passes through the point $(-2, 3)$, the y-coordinate of this point must satisfy the equation. Therefore, $c = 3$.
The equation of the line parallel to the x-axis and passing through $(-2, 3)$ is $y = 3$.
A line parallel to the y-axis has the form $x = c'$, where $c'$ is a constant. Since the line passes through the point $(-2, 3)$, the x-coordinate of this point must satisfy the equation. Therefore, $c' = -2$.
The equation of the line parallel to the y-axis and passing through $(-2, 3)$ is $x = -2$.
The equations of the lines parallel to the axes and passing through $(-2, 3)$ are $y = 3$ (parallel to the x-axis) and $x = -2$ (parallel to the y-axis).
Example 7: Find the equation of the line through (– 2, 3) with slope – 4.
Answer:
Given:
The line passes through the point $(x_1, y_1) = (-2, 3)$.
The slope of the line is $m = -4$.
To Find:
The equation of the line.
Solution:
We can use the point-slope form of the equation of a line, which is given by:
$y - y_1 = m(x - x_1)$
Substitute the given point $(-2, 3)$ for $(x_1, y_1)$ and the slope $m = -4$ into the formula:
$y - 3 = -4(x - (-2))$
$y - 3 = -4(x + 2)$
Now, simplify the equation:
$y - 3 = -4x - 8$
To get the equation in the general form $Ax + By + C = 0$, move all terms to one side:
$y - 3 + 4x + 8 = 0$
$4x + y + 5 = 0$
Alternatively, we could express the equation in slope-intercept form ($y = mx + c$).
Starting from $y - 3 = -4(x + 2)$:
$y - 3 = -4x - 8$
Add 3 to both sides:
$y = -4x - 8 + 3$
$y = -4x - 5$
The equation of the line through $(-2, 3)$ with slope $-4$ is $4x + y + 5 = 0$ or $y = -4x - 5$.
Example 8: Write the equation of the line through the points (1, –1) and (3, 5).
Answer:
Given:
The line passes through the points $A(1, -1)$ and $B(3, 5)$.
To Find:
The equation of the line passing through the given points.
Solution:
First, we find the slope of the line passing through the points $(x_1, y_1) = (1, -1)$ and $(x_2, y_2) = (3, 5)$.
The slope ($m$) is given by the formula:
$m = \frac{y_2 - y_1}{x_2 - x_1}$
Substitute the coordinates of points A and B:
$m = \frac{5 - (-1)}{3 - 1}$
$m = \frac{5 + 1}{2}$
$m = \frac{6}{2}$
$m = 3$
Now, we use the point-slope form of the equation of a line: $y - y_1 = m(x - x_1)$. We can use either point A or point B. Let's use point A $(1, -1)$ and the slope $m = 3$.
$y - (-1) = 3(x - 1)$
$y + 1 = 3x - 3$
To write the equation in the general form $Ax + By + C = 0$, move all terms to one side:
$3x - y - 3 - 1 = 0$
$3x - y - 4 = 0$
Alternatively, using the two-point form of the equation of a line:
$\frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}$
Substitute the coordinates of points A $(1, -1)$ and B $(3, 5)$:
$\frac{y - (-1)}{5 - (-1)} = \frac{x - 1}{3 - 1}$
$\frac{y + 1}{5 + 1} = \frac{x - 1}{2}$
$\frac{y + 1}{6} = \frac{x - 1}{2}$
Multiply both sides by 6 to eliminate the denominators:
$\cancel{6} \times \frac{y + 1}{\cancel{6}} = \cancel{6}^3 \times \frac{x - 1}{\cancel{2}}$
$y + 1 = 3(x - 1)$
$y + 1 = 3x - 3$
Rearrange to the general form:
$3x - y - 3 - 1 = 0$
$3x - y - 4 = 0$
The equation of the line through the points $(1, -1)$ and $(3, 5)$ is $3x - y - 4 = 0$.
Example 9: Write the equation of the lines for which tan θ = $\frac{1}{2}$, where θ is the inclination of the line and
(i) y-intercept is $-\frac{3}{2}$
(ii) x-intercept is 4.
Answer:
Given:
The tangent of the inclination of the line is $\tan \theta = \frac{1}{2}$.
The slope of the line is $m = \tan \theta$.
So, the slope is $m = \frac{1}{2}$.
To Find:
The equation of the line for the given conditions:
(i) y-intercept $c = -\frac{3}{2}$.
(ii) x-intercept is 4.
Solution:
(i) Line with slope $m = \frac{1}{2}$ and y-intercept $c = -\frac{3}{2}$.
We use the slope-intercept form of the equation of a line: $y = mx + c$.
Substitute the given values of $m$ and $c$:
$y = \frac{1}{2}x + \left(-\frac{3}{2}\right)$
$y = \frac{1}{2}x - \frac{3}{2}$
To eliminate the denominators, multiply the entire equation by 2:
$2y = 2 \times \left(\frac{1}{2}x\right) - 2 \times \left(\frac{3}{2}\right)$
$2y = x - 3$
Rearrange the terms to the general form $Ax + By + C = 0$:
$x - 2y - 3 = 0$
(ii) Line with slope $m = \frac{1}{2}$ and x-intercept is 4.
An x-intercept of 4 means the line passes through the point $(4, 0)$.
We have a point on the line $(x_1, y_1) = (4, 0)$ and the slope $m = \frac{1}{2}$.
We use the point-slope form of the equation of a line: $y - y_1 = m(x - x_1)$.
Substitute the given point and slope into the formula:
$y - 0 = \frac{1}{2}(x - 4)$
$y = \frac{1}{2}(x - 4)$
Multiply both sides by 2:
$2y = x - 4$
Rearrange the terms to the general form $Ax + By + C = 0$:
$x - 2y - 4 = 0$
The equation of the line for case (i) is $x - 2y - 3 = 0$.
The equation of the line for case (ii) is $x - 2y - 4 = 0$.
Example 10: Find the equation of the line, which makes intercepts –3 and 2 on the x- and y-axes respectively.
Answer:
Given:
The x-intercept of the line is $a = -3$.
The y-intercept of the line is $b = 2$.
To Find:
The equation of the line.
Solution:
We can use the intercept form of the equation of a line, which is given by:
$\frac{x}{a} + \frac{y}{b} = 1$
where $a$ is the x-intercept and $b$ is the y-intercept.
Substitute the given values of the x-intercept ($a = -3$) and the y-intercept ($b = 2$) into the formula:
$\frac{x}{-3} + \frac{y}{2} = 1$
To eliminate the denominators, we find the least common multiple (LCM) of 3 and 2, which is 6. Multiply both sides of the equation by 6:
$6 \times \left(\frac{x}{-3} + \frac{y}{2}\right) = 6 \times 1$
$6 \times \frac{x}{-3} + 6 \times \frac{y}{2} = 6$
Simplify the terms:
$\cancel{6}^{\;2} \times \frac{x}{\cancel{-3}} + \cancel{6}^{\;3} \times \frac{y}{\cancel{2}} = 6$
$-2x + 3y = 6$
To write the equation in the standard form $Ax + By + C = 0$, we can move all terms to one side. Let's move the terms to the left side:
$-2x + 3y - 6 = 0$
Alternatively, we can multiply by -1 to make the coefficient of $x$ positive:
$2x - 3y + 6 = 0$
Alternatively, we can note that the x-intercept is -3 means the line passes through $(-3, 0)$, and the y-intercept is 2 means the line passes through $(0, 2)$. We can find the slope using these two points:
$m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{2 - 0}{0 - (-3)} = \frac{2}{3}$
Using the slope-intercept form $y = mx + c$, where $m = \frac{2}{3}$ and $c = 2$ (the y-intercept):
$y = \frac{2}{3}x + 2$
Multiply by 3:
$3y = 2x + 6$
Rearrange to the general form:
$2x - 3y + 6 = 0$
The equation of the line is $2x - 3y + 6 = 0$.
Example 11: Find the equation of the line whose perpendicular distance from the origin is 4 units and the angle which the normal makes with positive direction of x-axis is 15°.
Answer:
Given:
The perpendicular distance of the line from the origin, $p = 4$ units.
The angle which the normal to the line makes with the positive direction of the x-axis, $\omega = 15^\circ$.
To Find:
The equation of the line.
Solution:
The equation of a line in the normal form is given by:
$x \cos \omega + y \sin \omega = p$
Here, we are given $p = 4$ and $\omega = 15^\circ$.
First, we need to find the values of $\cos 15^\circ$ and $\sin 15^\circ$.
We can write $15^\circ$ as $45^\circ - 30^\circ$.
Using the angle subtraction formulas for cosine and sine:
$\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$
$\sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta$
Let $\alpha = 45^\circ$ and $\beta = 30^\circ$.
$\cos 15^\circ = \cos (45^\circ - 30^\circ) = \cos 45^\circ \cos 30^\circ + \sin 45^\circ \sin 30^\circ$
$\cos 15^\circ = \left(\frac{1}{\sqrt{2}}\right) \left(\frac{\sqrt{3}}{2}\right) + \left(\frac{1}{\sqrt{2}}\right) \left(\frac{1}{2}\right)$
$\cos 15^\circ = \frac{\sqrt{3}}{2\sqrt{2}} + \frac{1}{2\sqrt{2}} = \frac{\sqrt{3}+1}{2\sqrt{2}}$
Similarly,
$\sin 15^\circ = \sin (45^\circ - 30^\circ) = \sin 45^\circ \cos 30^\circ - \cos 45^\circ \sin 30^\circ$
$\sin 15^\circ = \left(\frac{1}{\sqrt{2}}\right) \left(\frac{\sqrt{3}}{2}\right) - \left(\frac{1}{\sqrt{2}}\right) \left(\frac{1}{2}\right)$
$\sin 15^\circ = \frac{\sqrt{3}}{2\sqrt{2}} - \frac{1}{2\sqrt{2}} = \frac{\sqrt{3}-1}{2\sqrt{2}}$
Now, substitute the values of $p$, $\cos 15^\circ$, and $\sin 15^\circ$ into the normal form equation $x \cos \omega + y \sin \omega = p$:
$x \left(\frac{\sqrt{3}+1}{2\sqrt{2}}\right) + y \left(\frac{\sqrt{3}-1}{2\sqrt{2}}\right) = 4$
To simplify the equation, multiply both sides by $2\sqrt{2}$:
$2\sqrt{2} \left[ x \left(\frac{\sqrt{3}+1}{2\sqrt{2}}\right) + y \left(\frac{\sqrt{3}-1}{2\sqrt{2}}\right) \right] = 4 \times 2\sqrt{2}$
$(\sqrt{3}+1)x + (\sqrt{3}-1)y = 8\sqrt{2}$
Therefore, the required equation of the line is $(\sqrt{3}+1)x + (\sqrt{3}-1)y = 8\sqrt{2}$.
Example 12: The Fahrenheit temperature F and absolute temperature K satisfy a linear equation. Given that K = 273 when F = 32 and that K = 373 when F = 212. Express K in terms of F and find the value of F, when K = 0.
Answer:
Given:
The Fahrenheit temperature (F) and absolute temperature (K) satisfy a linear equation.
We are given two points on this line:
Point 1: When $F = 32$, $K = 273$. So, $(F_1, K_1) = (32, 273)$.
Point 2: When $F = 212$, $K = 373$. So, $(F_2, K_2) = (212, 373)$.
To Find:
1. Express K in terms of F.
2. Find the value of F when K = 0.
Solution:
Since F and K satisfy a linear equation, we can represent the relationship as $K = mF + c$, where $m$ is the slope and $c$ is the K-intercept.
Using the two given points, we can form two equations:
$273 = m(32) + c$
...(i)
$373 = m(212) + c$
...(ii)
To find the slope $m$, we can subtract equation (i) from equation (ii):
$(373 - 273) = (212m + c) - (32m + c)$
$100 = 212m - 32m$
$100 = 180m$
$m = \frac{100}{180} = \frac{10}{18} = \frac{5}{9}$
Now, substitute the value of $m = \frac{5}{9}$ into equation (i) to find $c$:
$273 = \frac{5}{9} (32) + c$
$273 = \frac{160}{9} + c$
$c = 273 - \frac{160}{9}$
$c = \frac{273 \times 9 - 160}{9}$
$c = \frac{2457 - 160}{9}$
$c = \frac{2297}{9}$
So, the linear equation expressing K in terms of F is:
$K = \frac{5}{9}F + \frac{2297}{9}$
Now, we need to find the value of F when K = 0.
Substitute $K = 0$ into the equation:
$0 = \frac{5}{9}F + \frac{2297}{9}$
Multiply the entire equation by 9 to eliminate the denominators:
$9 \times 0 = 9 \times \left( \frac{5}{9}F + \frac{2297}{9} \right)$
$0 = 5F + 2297$
Rearrange the equation to solve for F:
$5F = -2297$
$F = -\frac{2297}{5}$
$F = -459.4$
Therefore, the value of F when K = 0 is -459.4.
Exercise 10.2
In Exercises 1 to 8, find the equation of the line which satisfy the given conditions:
Question 1. Write the equations for the x-and y-axes.
Answer:
Equation of the x-axis:
Any point on the x-axis has its y-coordinate equal to 0. For example, (1, 0), (-2, 0), (5, 0) all lie on the x-axis.
Therefore, the equation of the x-axis is y = 0.
Equation of the y-axis:
Any point on the y-axis has its x-coordinate equal to 0. For example, (0, 3), (0, -4), (0, 1) all lie on the y-axis.
Therefore, the equation of the y-axis is x = 0.
Question 2. Passing through the point (– 4, 3) with slope $\frac{1}{2}$ .
Answer:
Given:
A point on the line $(x_1, y_1) = (-4, 3)$.
The slope of the line $m = \frac{1}{2}$.
To Find:
The equation of the line.
Solution:
We can use the point-slope form of the equation of a line, which is given by:
$y - y_1 = m(x - x_1)$
Substitute the given values $x_1 = -4$, $y_1 = 3$, and $m = \frac{1}{2}$ into the formula:
$y - 3 = \frac{1}{2} (x - (-4))$
$y - 3 = \frac{1}{2} (x + 4)$
To eliminate the fraction, multiply both sides of the equation by 2:
$2(y - 3) = 2 \times \frac{1}{2} (x + 4)$
$2y - 6 = x + 4$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$x - 2y + 4 + 6 = 0$
$x - 2y + 10 = 0$
Therefore, the required equation of the line is $x - 2y + 10 = 0$.
Question 3. Passing through (0, 0) with slope m.
Answer:
Given:
A point on the line $(x_1, y_1) = (0, 0)$ (the origin).
The slope of the line is $m$.
To Find:
The equation of the line.
Solution:
We can use the point-slope form of the equation of a line, which is given by:
$y - y_1 = m(x - x_1)$
Substitute the given values $x_1 = 0$, $y_1 = 0$, and the slope $m$ into the formula:
$y - 0 = m(x - 0)$
$y = m(x)$
$y = mx$
Alternatively, we can use the slope-intercept form $y = mx + c$. Since the line passes through the origin (0, 0), the y-intercept $c$ is 0. Substituting $c=0$ into the slope-intercept form gives $y = mx + 0$, which simplifies to $y = mx$.
Therefore, the required equation of the line is $y = mx$.
Question 4. Passing through (2, 2$\sqrt{3}$) and inclined with the x-axis at an angle of 75°.
Answer:
Given:
A point on the line $(x_1, y_1) = (2, 2\sqrt{3})$.
The angle of inclination with the x-axis, $\theta = 75^\circ$.
To Find:
The equation of the line.
Solution:
First, we need to find the slope ($m$) of the line using the angle of inclination $\theta$.
The slope $m$ is given by $m = \tan \theta$.
Here, $\theta = 75^\circ$. So, $m = \tan 75^\circ$.
We can find $\tan 75^\circ$ by expressing $75^\circ$ as $45^\circ + 30^\circ$.
Using the tangent addition formula: $\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta}$
$m = \tan(45^\circ + 30^\circ) = \frac{\tan 45^\circ + \tan 30^\circ}{1 - \tan 45^\circ \tan 30^\circ}$
We know that $\tan 45^\circ = 1$ and $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
$m = \frac{1 + \frac{1}{\sqrt{3}}}{1 - (1)\left(\frac{1}{\sqrt{3}}\right)} = \frac{\frac{\sqrt{3}+1}{\sqrt{3}}}{\frac{\sqrt{3}-1}{\sqrt{3}}}$
$m = \frac{\sqrt{3}+1}{\sqrt{3}-1}$
To rationalize the denominator, multiply the numerator and denominator by $(\sqrt{3}+1)$:
$m = \frac{\sqrt{3}+1}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1} = \frac{(\sqrt{3}+1)^2}{(\sqrt{3})^2 - 1^2}$
$m = \frac{3 + 1 + 2\sqrt{3}}{3 - 1} = \frac{4 + 2\sqrt{3}}{2}$
$m = 2 + \sqrt{3}$
Now we have the slope $m = 2 + \sqrt{3}$ and a point $(x_1, y_1) = (2, 2\sqrt{3})$.
We use the point-slope form of the equation of a line: $y - y_1 = m(x - x_1)$.
Substitute the values:
$y - 2\sqrt{3} = (2 + \sqrt{3})(x - 2)$
Expand the right side:
$y - 2\sqrt{3} = (2 + \sqrt{3})x - 2(2 + \sqrt{3})$
$y - 2\sqrt{3} = (2 + \sqrt{3})x - 4 - 2\sqrt{3}$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$(2 + \sqrt{3})x - y - 4 - 2\sqrt{3} + 2\sqrt{3} = 0$
$(2 + \sqrt{3})x - y - 4 = 0$
Therefore, the required equation of the line is $(2 + \sqrt{3})x - y - 4 = 0$.
Question 5. Intersecting the x-axis at a distance of 3 units to the left of origin with slope –2.
Answer:
Given:
The line intersects the x-axis at a distance of 3 units to the left of the origin. This means the x-intercept is -3. The point of intersection with the x-axis is $(-3, 0)$.
The slope of the line, $m = -2$.
To Find:
The equation of the line.
Solution:
We have a point on the line $(x_1, y_1) = (-3, 0)$ and the slope $m = -2$.
We can use the point-slope form of the equation of a line, which is given by:
$y - y_1 = m(x - x_1)$
Substitute the given values $x_1 = -3$, $y_1 = 0$, and $m = -2$ into the formula:
$y - 0 = -2(x - (-3))$
$y = -2(x + 3)$
Expand the right side:
$y = -2x - 6$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$2x + y + 6 = 0$
Therefore, the required equation of the line is $2x + y + 6 = 0$.
Question 6. Intersecting the y-axis at a distance of 2 units above the origin and making an angle of 30o with positive direction of the x-axis.
Answer:
Given:
The line intersects the y-axis at a distance of 2 units above the origin. This means the y-intercept is $c = 2$. The point of intersection with the y-axis is $(0, 2)$.
The angle made with the positive direction of the x-axis is $\theta = 30^\circ$.
To Find:
The equation of the line.
Solution:
First, we find the slope ($m$) of the line using the angle of inclination $\theta$.
The slope $m$ is given by $m = \tan \theta$.
Here, $\theta = 30^\circ$. So, $m = \tan 30^\circ$.
$m = \frac{1}{\sqrt{3}}$
Now we have the slope $m = \frac{1}{\sqrt{3}}$ and the y-intercept $c = 2$.
We can use the slope-intercept form of the equation of a line, which is given by:
$y = mx + c$
Substitute the values $m = \frac{1}{\sqrt{3}}$ and $c = 2$ into the formula:
$y = \frac{1}{\sqrt{3}}x + 2$
To eliminate the fraction, multiply both sides of the equation by $\sqrt{3}$:
$\sqrt{3} y = \sqrt{3} \left( \frac{1}{\sqrt{3}}x + 2 \right)$
$\sqrt{3} y = x + 2\sqrt{3}$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$x - \sqrt{3} y + 2\sqrt{3} = 0$
Therefore, the required equation of the line is $x - \sqrt{3} y + 2\sqrt{3} = 0$.
Question 7. Passing through the points (–1, 1) and (2, – 4).
Answer:
Given:
Two points on the line: $(x_1, y_1) = (-1, 1)$ and $(x_2, y_2) = (2, -4)$.
To Find:
The equation of the line.
Solution:
We can use the two-point form of the equation of a line, which is given by:
$\frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1}$
Substitute the coordinates of the given points:
$x_1 = -1, y_1 = 1$
$x_2 = 2, y_2 = -4$
$\frac{y - 1}{x - (-1)} = \frac{-4 - 1}{2 - (-1)}$
$\frac{y - 1}{x + 1} = \frac{-5}{2 + 1}$
$\frac{y - 1}{x + 1} = \frac{-5}{3}$
Now, cross-multiply to simplify the equation:
$3(y - 1) = -5(x + 1)$
$3y - 3 = -5x - 5$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$5x + 3y - 3 + 5 = 0$
$5x + 3y + 2 = 0$
Therefore, the required equation of the line is $5x + 3y + 2 = 0$.
Alternate Solution (Using Slope-Point Form):
First, calculate the slope ($m$) of the line using the two points:
$m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-4 - 1}{2 - (-1)} = \frac{-5}{3}$
Now, use the point-slope form $y - y_1 = m(x - x_1)$ with one of the points, say $(-1, 1)$:
$y - 1 = -\frac{5}{3}(x - (-1))$
$y - 1 = -\frac{5}{3}(x + 1)$
Multiply both sides by 3:
$3(y - 1) = -5(x + 1)$
$3y - 3 = -5x - 5$
Rearrange the terms:
$5x + 3y - 3 + 5 = 0$
$5x + 3y + 2 = 0$
This gives the same equation $5x + 3y + 2 = 0$.
Question 8. Perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive x-axis is 30°.
Answer:
Given:
The perpendicular distance of the line from the origin, $p = 5$ units.
The angle made by the perpendicular (normal) to the line with the positive x-axis, $\omega = 30^\circ$.
To Find:
The equation of the line.
Solution:
We can use the normal form of the equation of a line, which is given by:
$x \cos \omega + y \sin \omega = p$
Substitute the given values $p = 5$ and $\omega = 30^\circ$ into the formula.
We need the values of $\cos 30^\circ$ and $\sin 30^\circ$.
$\cos 30^\circ = \frac{\sqrt{3}}{2}$
$\sin 30^\circ = \frac{1}{2}$
Substitute these trigonometric values into the normal form equation:
$x \left(\frac{\sqrt{3}}{2}\right) + y \left(\frac{1}{2}\right) = 5$
To simplify the equation, multiply both sides by 2:
$2 \left[ x \left(\frac{\sqrt{3}}{2}\right) + y \left(\frac{1}{2}\right) \right] = 2 \times 5$
$\sqrt{3}x + y = 10$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$\sqrt{3}x + y - 10 = 0$
Therefore, the required equation of the line is $\sqrt{3}x + y - 10 = 0$.
Question 9. The vertices of ∆ PQR are P (2, 1), Q (–2, 3) and R (4, 5). Find equation of the median through the vertex R.
Answer:
Given:
The vertices of ∆ PQR are P(2, 1), Q(–2, 3), and R(4, 5).
To Find:
The equation of the median through the vertex R.
Solution:
The median through the vertex R connects R to the midpoint of the opposite side PQ.
Let M be the midpoint of the side PQ.
The coordinates of the midpoint M are found using the midpoint formula:
$M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$
Using the coordinates of P(2, 1) and Q(–2, 3):
$M_x = \frac{2 + (-2)}{2} = \frac{0}{2} = 0$
$M_y = \frac{1 + 3}{2} = \frac{4}{2} = 2$
So, the coordinates of the midpoint M are (0, 2).
Now, we need to find the equation of the line passing through the points R(4, 5) and M(0, 2). This line is the median through R.
We can use the two-point form of the equation of a line:
$\frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1}$
Let $(x_1, y_1) = (4, 5)$ (point R) and $(x_2, y_2) = (0, 2)$ (point M).
$\frac{y - 5}{x - 4} = \frac{2 - 5}{0 - 4}$
$\frac{y - 5}{x - 4} = \frac{-3}{-4}$
$\frac{y - 5}{x - 4} = \frac{3}{4}$
Cross-multiply:
$4(y - 5) = 3(x - 4)$
$4y - 20 = 3x - 12$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$3x - 4y - 12 + 20 = 0$
$3x - 4y + 8 = 0$
Therefore, the equation of the median through the vertex R is $3x - 4y + 8 = 0$.
Question 10. Find the equation of the line passing through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).
Answer:
Given:
The required line passes through the point $P(-3, 5)$.
The required line is perpendicular to the line passing through the points $A(2, 5)$ and $B(-3, 6)$.
To Find:
The equation of the line passing through $P(-3, 5)$.
Solution:
First, find the slope of the line passing through points $A(2, 5)$ and $B(-3, 6)$. Let this slope be $m_1$.
Using the slope formula $m = \frac{y_2 - y_1}{x_2 - x_1}$:
$m_1 = \frac{6 - 5}{-3 - 2} = \frac{1}{-5} = -\frac{1}{5}$
Let the slope of the required line be $m_2$.
Since the required line is perpendicular to the line AB, the product of their slopes must be -1.
$m_1 \times m_2 = -1$
$\left(-\frac{1}{5}\right) \times m_2 = -1$
$m_2 = \frac{-1}{-\frac{1}{5}}$
$m_2 = 5$
Now we have the slope of the required line ($m_2 = 5$) and a point it passes through $P(-3, 5)$.
We can use the point-slope form of the equation of a line: $y - y_1 = m(x - x_1)$.
Substitute the point $(x_1, y_1) = (-3, 5)$ and the slope $m = 5$:
$y - 5 = 5(x - (-3))$
$y - 5 = 5(x + 3)$
$y - 5 = 5x + 15$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$5x - y + 15 + 5 = 0$
$5x - y + 20 = 0$
Therefore, the required equation of the line is $5x - y + 20 = 0$.
Question 11. A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1: n. Find the equation of the line.
Answer:
Given:
The required line is perpendicular to the line segment joining the points $A(1, 0)$ and $B(2, 3)$.
The required line passes through a point P which divides the line segment AB in the ratio $1:n$.
To Find:
The equation of the required line.
Solution:
First, let's find the slope of the line segment joining A(1, 0) and B(2, 3). Let this slope be $m_1$.
$m_1 = \frac{y_2 - y_1}{x_2 - x_1} = \frac{3 - 0}{2 - 1} = \frac{3}{1} = 3$
Let the slope of the required line be $m_2$. Since the required line is perpendicular to the segment AB, the product of their slopes is -1.
$m_1 \times m_2 = -1$
$3 \times m_2 = -1$
$m_2 = -\frac{1}{3}$
Next, let's find the coordinates of the point P(x, y) that divides the line segment joining $A(1, 0)$ and $B(2, 3)$ in the ratio $1:n$.
Using the section formula:
$P(x, y) = \left( \frac{n x_1 + 1 x_2}{1 + n}, \frac{n y_1 + 1 y_2}{1 + n} \right)$
Here, $(x_1, y_1) = (1, 0)$ and $(x_2, y_2) = (2, 3)$.
$x = \frac{n(1) + 1(2)}{1 + n} = \frac{n + 2}{n + 1}$
$y = \frac{n(0) + 1(3)}{1 + n} = \frac{0 + 3}{n + 1} = \frac{3}{n + 1}$
So, the point P is $\left( \frac{n + 2}{n + 1}, \frac{3}{n + 1} \right)$.
Now, we need to find the equation of the line passing through the point $P\left( \frac{n + 2}{n + 1}, \frac{3}{n + 1} \right)$ with slope $m_2 = -\frac{1}{3}$.
Using the point-slope form of the equation of a line: $y - y_P = m_2(x - x_P)$.
$y - \frac{3}{n + 1} = -\frac{1}{3} \left( x - \frac{n + 2}{n + 1} \right)$
To eliminate the denominators, multiply both sides by $3(n + 1)$:
$3(n + 1) \left( y - \frac{3}{n + 1} \right) = 3(n + 1) \left[ -\frac{1}{3} \left( x - \frac{n + 2}{n + 1} \right) \right]$
$3(n + 1)y - 3(n + 1) \cdot \frac{3}{n + 1} = -(n + 1) \left( x - \frac{n + 2}{n + 1} \right)$
$3(n + 1)y - 9 = -(n + 1)x + (n + 1) \cdot \frac{n + 2}{n + 1}$
$3(n + 1)y - 9 = -(n + 1)x + (n + 2)$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$(n + 1)x + 3(n + 1)y - 9 - (n + 2) = 0$
$(n + 1)x + 3(n + 1)y - 9 - n - 2 = 0$
$(n + 1)x + 3(n + 1)y - n - 11 = 0$
Therefore, the required equation of the line is $(n + 1)x + 3(n + 1)y - n - 11 = 0$.
Question 12. Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
Answer:
Given:
A line cuts off equal intercepts on the coordinate axes.
The line passes through the point (2, 3).
To Find:
The equation of the line.
Solution:
The equation of a line in intercept form is:
$\frac{x}{a} + \frac{y}{b} = 1$
where $a$ is the x-intercept and $b$ is the y-intercept.
Case 1: Non-zero intercepts
Given that the line cuts off equal intercepts, we have $a = b$. Assuming the intercepts are non-zero ($a \neq 0$), the equation becomes:
$\frac{x}{a} + \frac{y}{a} = 1$
Multiply by $a$:
$x + y = a$
Since the line passes through the point (2, 3), substitute $x = 2$ and $y = 3$ into this equation:
$2 + 3 = a$
$a = 5$
Substitute the value of $a$ back into the equation $x + y = a$:
$x + y = 5$
This can also be written in the general form as $x + y - 5 = 0$.
Case 2: Zero intercepts
If the intercepts are equal, they could both be zero ($a = 0, b = 0$). This means the line passes through the origin (0, 0).
The line also passes through the point (2, 3).
The equation of a line passing through the origin (0, 0) and another point $(x_1, y_1)$ is $y = mx$, where the slope $m = \frac{y_1 - 0}{x_1 - 0} = \frac{y_1}{x_1}$.
Using the point (2, 3):
$m = \frac{3}{2}$
So, the equation is $y = \frac{3}{2}x$.
Rearranging, we get $2y = 3x$, or $3x - 2y = 0$.
This line $3x - 2y = 0$ indeed passes through (2, 3) since $3(2) - 2(3) = 6 - 6 = 0$. Its x-intercept (set $y=0$) is $3x=0 \implies x=0$, and its y-intercept (set $x=0$) is $-2y=0 \implies y=0$. The intercepts are equal (both are 0).
Conclusion:
The phrase "cuts off equal intercepts" usually implies the use of the intercept form $\frac{x}{a} + \frac{y}{b} = 1$, which assumes $a \neq 0$ and $b \neq 0$. Under this standard interpretation, the equation is:
$x + y = 5$ or $x + y - 5 = 0$.
However, the line $3x - 2y = 0$ also satisfies the condition of having equal intercepts (both 0) and passing through (2, 3).
Usually, the intended answer in such problems is the one derived from the non-zero intercept case.
Question 13. Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
Answer:
Given:
The line passes through the point P(2, 2).
The sum of the intercepts cut off by the line on the coordinate axes is 9.
To Find:
The equation of the line.
Solution:
Let the equation of the line in the intercept form be:
$\frac{x}{a} + \frac{y}{b} = 1$
...(i)
where $a$ is the x-intercept and $b$ is the y-intercept.
We are given that the sum of the intercepts is 9:
$a + b = 9$
...(ii)
From equation (ii), we can express $b$ in terms of $a$:
$b = 9 - a$
Since the line passes through the point (2, 2), this point must satisfy the equation of the line (i):
$\frac{2}{a} + \frac{2}{b} = 1$
Substitute $b = 9 - a$ into this equation:
$\frac{2}{a} + \frac{2}{9 - a} = 1$
To solve for $a$, multiply the entire equation by $a(9 - a)$:
$2(9 - a) + 2a = a(9 - a)$
$18 - 2a + 2a = 9a - a^2$
$18 = 9a - a^2$
Rearrange into a quadratic equation:
$a^2 - 9a + 18 = 0$
Factor the quadratic equation:
$(a - 3)(a - 6) = 0$
This gives two possible values for $a$: $a = 3$ or $a = 6$.
Now, find the corresponding values for $b$ using $b = 9 - a$:
Case 1: If $a = 3$, then $b = 9 - 3 = 6$.
Substitute $a = 3$ and $b = 6$ into the intercept form (i):
$\frac{x}{3} + \frac{y}{6} = 1$
Multiply by the least common multiple (6) to clear the denominators:
$2x + y = 6$
Or, in general form: $2x + y - 6 = 0$.
Case 2: If $a = 6$, then $b = 9 - 6 = 3$.
Substitute $a = 6$ and $b = 3$ into the intercept form (i):
$\frac{x}{6} + \frac{y}{3} = 1$
Multiply by the least common multiple (6) to clear the denominators:
$x + 2y = 6$
Or, in general form: $x + 2y - 6 = 0$.
Thus, there are two possible lines that satisfy the given conditions.
The required equations of the lines are $2x + y - 6 = 0$ and $x + 2y - 6 = 0$.
Question 14. Find equation of the line through the point (0, 2) making an angle $\frac{2\pi}{3}$ with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.
Answer:
Given:
For the first line:
Passes through the point $P(0, 2)$.
Angle of inclination with the positive x-axis, $\theta = \frac{2\pi}{3}$ radians (or $120^\circ$).
For the second line:
Parallel to the first line.
Crosses the y-axis at a distance of 2 units below the origin (y-intercept is -2).
To Find:
1. Equation of the first line.
2. Equation of the second line (parallel to the first).
Solution:
Finding the equation of the first line:
First, find the slope ($m_1$) of the first line using the angle of inclination $\theta = \frac{2\pi}{3}$.
$m_1 = \tan(\theta) = \tan\left(\frac{2\pi}{3}\right)$
Since $\frac{2\pi}{3} = 120^\circ$, we have:
$m_1 = \tan(120^\circ) = \tan(180^\circ - 60^\circ) = -\tan(60^\circ) = -\sqrt{3}$
The line passes through the point (0, 2). This point is the y-intercept, so $c_1 = 2$.
We can use the slope-intercept form of the equation of a line: $y = m_1 x + c_1$.
Substitute $m_1 = -\sqrt{3}$ and $c_1 = 2$:
$y = -\sqrt{3}x + 2$
Rearrange to the general form $Ax + By + C = 0$:
$\sqrt{3}x + y - 2 = 0$
So, the equation of the first line is $\sqrt{3}x + y - 2 = 0$.
Finding the equation of the second line:
The second line is parallel to the first line. Parallel lines have the same slope.
Therefore, the slope of the second line ($m_2$) is equal to the slope of the first line ($m_1$).
$m_2 = m_1 = -\sqrt{3}$
The second line crosses the y-axis at a distance of 2 units below the origin. This means the y-intercept of the second line ($c_2$) is -2.
Using the slope-intercept form $y = m_2 x + c_2$:
Substitute $m_2 = -\sqrt{3}$ and $c_2 = -2$:
$y = -\sqrt{3}x - 2$
Rearrange to the general form $Ax + By + C = 0$:
$\sqrt{3}x + y + 2 = 0$
So, the equation of the second line is $\sqrt{3}x + y + 2 = 0$.
Final Answer:
The equation of the line through (0, 2) making an angle $\frac{2\pi}{3}$ with the positive x-axis is $\sqrt{3}x + y - 2 = 0$.
The equation of the line parallel to it and crossing the y-axis 2 units below the origin is $\sqrt{3}x + y + 2 = 0$.
Question 15. The perpendicular from the origin to a line meets it at the point (–2, 9), find the equation of the line.
Answer:
Given:
The origin O is at (0, 0).
The perpendicular line segment from the origin O meets the required line at the point P(–2, 9).
To Find:
The equation of the required line.
Solution:
The line segment joining the origin O(0, 0) and the point P(–2, 9) is perpendicular to the required line.
First, let's find the slope of the line segment OP. Let this slope be $m_{OP}$.
$m_{OP} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{9 - 0}{-2 - 0} = \frac{9}{-2} = -\frac{9}{2}$
Let the slope of the required line be $m_{line}$.
Since the required line is perpendicular to the line segment OP, the product of their slopes is -1.
$m_{OP} \times m_{line} = -1$
$\left(-\frac{9}{2}\right) \times m_{line} = -1$
$m_{line} = \frac{-1}{-\frac{9}{2}} = \frac{2}{9}$
The required line passes through the point P(–2, 9) and has a slope $m_{line} = \frac{2}{9}$.
We can use the point-slope form of the equation of a line: $y - y_1 = m(x - x_1)$.
Substitute the point $(x_1, y_1) = (–2, 9)$ and the slope $m = \frac{2}{9}$:
$y - 9 = \frac{2}{9}(x - (-2))$
$y - 9 = \frac{2}{9}(x + 2)$
Multiply both sides by 9 to eliminate the fraction:
$9(y - 9) = 2(x + 2)$
$9y - 81 = 2x + 4$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$2x - 9y + 4 + 81 = 0$
$2x - 9y + 85 = 0$
Therefore, the required equation of the line is $2x - 9y + 85 = 0$.
Question 16. The length L (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L = 125.134 when C = 110, express L in terms of C.
Answer:
Given:
The length L of a copper rod is a linear function of its Celsius temperature C.
We are given two points representing (Temperature C, Length L):
Point 1: $(C_1, L_1) = (20, 124.942)$
Point 2: $(C_2, L_2) = (110, 125.134)$
To Find:
An equation expressing L in terms of C.
Solution:
Since L is a linear function of C, the relationship can be represented by the equation $L = mC + b$, where $m$ is the slope and $b$ is the L-intercept.
We can use the two given points to find the equation of the line.
First, calculate the slope $m$:
$m = \frac{L_2 - L_1}{C_2 - C_1}$
$m = \frac{125.134 - 124.942}{110 - 20}$
$m = \frac{0.192}{90}$
Let's simplify the slope as a fraction:
$m = \frac{192}{90000} = \frac{96}{45000} = \frac{48}{22500} = \frac{24}{11250} = \frac{12}{5625} = \frac{4}{1875}$
So, the slope $m = \frac{4}{1875}$.
Now we can use the point-slope form of a linear equation: $L - L_1 = m(C - C_1)$.
Using the point $(C_1, L_1) = (20, 124.942)$ and the slope $m = \frac{4}{1875}$:
$L - 124.942 = \frac{4}{1875}(C - 20)$
To express L in terms of C, we rearrange the equation to the form $L = mC + b$:
$L = \frac{4}{1875}(C - 20) + 124.942$
$L = \frac{4}{1875}C - \frac{4 \times 20}{1875} + 124.942$
$L = \frac{4}{1875}C - \frac{80}{1875} + 124.942$
Simplify the fraction $\frac{80}{1875}$ by dividing numerator and denominator by 5 twice:
$\frac{80}{1875} = \frac{16}{375}$
Express 124.942 as a fraction: $124.942 = \frac{124942}{1000} = \frac{62471}{500}$
$L = \frac{4}{1875}C - \frac{16}{375} + \frac{62471}{500}$
To combine the constant terms, find a common denominator for 375 and 500. The least common multiple (LCM) is 1500.
$L = \frac{4}{1875}C - \frac{16 \times 4}{375 \times 4} + \frac{62471 \times 3}{500 \times 3}$
$L = \frac{4}{1875}C - \frac{64}{1500} + \frac{187413}{1500}$
$L = \frac{4}{1875}C + \frac{187413 - 64}{1500}$
$L = \frac{4}{1875}C + \frac{187349}{1500}$
Therefore, the linear equation expressing L in terms of C is $L = \frac{4}{1875}C + \frac{187349}{1500}$.
Alternate Presentation (using point-slope form):
The relationship can also be expressed using the point-slope form derived earlier:
$L - 124.942 = \frac{4}{1875}(C - 20)$
Or using the other point:
$L - 125.134 = \frac{4}{1875}(C - 110)$
However, the form $L = mC + b$ is generally preferred when asked to express one variable in terms of another.
Question 17. The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs 17/litre?
Answer:
Given:
Let P be the selling price per litre and D be the weekly demand in litres.
There is a linear relationship between P and D.
We have two points (P, D) on this linear relationship:
Point 1: When P = 14, D = 980. So, $(P_1, D_1) = (14, 980)$.
Point 2: When P = 16, D = 1220. So, $(P_2, D_2) = (16, 1220)$.
To Find:
The weekly demand (D) when the selling price (P) is $\textsf{₹}$ 17/litre.
Solution:
Since the relationship between selling price (P) and demand (D) is linear, we can represent it by the equation $D = mP + c$, where $m$ is the slope and $c$ is the D-intercept.
First, calculate the slope ($m$) using the two given points:
$m = \frac{D_2 - D_1}{P_2 - P_1}$
$m = \frac{1220 - 980}{16 - 14}$
$m = \frac{240}{2}$
$m = 120$
Now, use the point-slope form of the linear equation, $D - D_1 = m(P - P_1)$, using Point 1 (14, 980) and the slope $m = 120$:
$D - 980 = 120(P - 14)$
$D - 980 = 120P - 120 \times 14$
$D - 980 = 120P - 1680$
$D = 120P - 1680 + 980$
$D = 120P - 700$
This is the linear equation relating demand (D) and price (P).
We need to find the demand (D) when the price (P) is $\textsf{₹}$ 17/litre.
Substitute $P = 17$ into the equation $D = 120P - 700$:
$D = 120(17) - 700$
$D = 2040 - 700$
$D = 1340$
Therefore, the owner could sell 1340 litres of milk weekly at $\textsf{₹}$ 17/litre.
Question 18. P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is $\frac{x}{a}$ + $\frac{y}{b}$ = 2.
Answer:
Given:
A line segment lies between the coordinate axes.
P(a, b) is the midpoint of this line segment.
To Show:
The equation of the line is $\frac{x}{a} + \frac{y}{b} = 2$.
Proof:
Let the line intersect the x-axis at point A and the y-axis at point B.
Since point A is on the x-axis, its y-coordinate is 0. Let the coordinates of A be $(x_0, 0)$. This means the x-intercept is $x_0$.
Since point B is on the y-axis, its x-coordinate is 0. Let the coordinates of B be $(0, y_0)$. This means the y-intercept is $y_0$.
The line segment between the axes is the segment AB.
We are given that P(a, b) is the midpoint of the line segment AB.
Using the midpoint formula, the coordinates of the midpoint of AB are:
Midpoint = $\left( \frac{x_0 + 0}{2}, \frac{0 + y_0}{2} \right) = \left( \frac{x_0}{2}, \frac{y_0}{2} \right)$
Since P(a, b) is the midpoint, we can equate the coordinates:
$a = \frac{x_0}{2} \implies x_0 = 2a$
$b = \frac{y_0}{2} \implies y_0 = 2b$
So, the x-intercept of the line is $2a$ and the y-intercept of the line is $2b$.
The equation of a line in the intercept form is:
$\frac{x}{\text{x-intercept}} + \frac{y}{\text{y-intercept}} = 1$
Substitute the intercepts we found ($x_0 = 2a$ and $y_0 = 2b$):
$\frac{x}{2a} + \frac{y}{2b} = 1$
To obtain the required form, multiply both sides of the equation by 2:
$2 \left( \frac{x}{2a} + \frac{y}{2b} \right) = 2 \times 1$
$\frac{2x}{2a} + \frac{2y}{2b} = 2$
$\frac{x}{a} + \frac{y}{b} = 2$
Thus, the equation of the line is $\frac{x}{a} + \frac{y}{b} = 2$.
Hence Proved.
Question 19. Point R (h, k) divides a line segment between the axes in the ratio 1: 2. Find equation of the line.
Answer:
Given:
A line segment lies between the coordinate axes.
Point R(h, k) divides this line segment in the ratio 1:2.
To Find:
The equation of the line.
Solution:
Let the line intersect the x-axis at point A and the y-axis at point B.
The coordinates of A are $(x_0, 0)$ (x-intercept is $x_0$).
The coordinates of B are $(0, y_0)$ (y-intercept is $y_0$).
The line segment between the axes is AB.
The point R(h, k) divides the segment AB in the ratio 1:2. We assume the ratio is AR:RB = 1:2 (meaning R is closer to A on the x-axis).
Using the section formula for internal division:
$R(h, k) = \left( \frac{m x_B + n x_A}{m + n}, \frac{m y_B + n y_A}{m + n} \right)$
Here, $(x_A, y_A) = (x_0, 0)$, $(x_B, y_B) = (0, y_0)$, and the ratio $m:n = 1:2$.
$h = \frac{1(0) + 2(x_0)}{1 + 2} = \frac{2x_0}{3}$
$k = \frac{1(y_0) + 2(0)}{1 + 2} = \frac{y_0}{3}$
From these equations, we can express the intercepts $x_0$ and $y_0$ in terms of $h$ and $k$:
$2x_0 = 3h \implies x_0 = \frac{3h}{2}$
$y_0 = 3k$
So, the x-intercept of the line is $\frac{3h}{2}$ and the y-intercept is $3k$.
Now, use the intercept form of the equation of a line:
$\frac{x}{\text{x-intercept}} + \frac{y}{\text{y-intercept}} = 1$
Substitute the intercepts we found:
$\frac{x}{3h/2} + \frac{y}{3k} = 1$
Simplify the first term:
$\frac{2x}{3h} + \frac{y}{3k} = 1$
To clear the denominators, multiply the entire equation by the least common multiple, which is $3hk$:
$3hk \left( \frac{2x}{3h} \right) + 3hk \left( \frac{y}{3k} \right) = 3hk \times 1$
$k(2x) + h(y) = 3hk$
$2kx + hy = 3hk$
This can be rearranged to the general form $2kx + hy - 3hk = 0$.
Therefore, the required equation of the line is $2kx + hy = 3hk$.
Note: If the ratio was interpreted as BR:RA = 1:2 (meaning R is closer to B on the y-axis, so the ratio $m:n$ for AR:RB would be 2:1), the calculation would be:
$h = \frac{2(0) + 1(x_0)}{2 + 1} = \frac{x_0}{3} \implies x_0 = 3h$
$k = \frac{2(y_0) + 1(0)}{2 + 1} = \frac{2y_0}{3} \implies y_0 = \frac{3k}{2}$
The equation would be $\frac{x}{3h} + \frac{y}{3k/2} = 1$, which simplifies to $\frac{x}{3h} + \frac{2y}{3k} = 1$, or $kx + 2hy = 3hk$.
Assuming the standard interpretation AR:RB = 1:2, the answer is $2kx + hy = 3hk$.
Question 20. By using the concept of equation of a line, prove that the three points (3, 0), (– 2, – 2) and (8, 2) are collinear.
Answer:
Given:
Three points: A(3, 0), B(–2, –2), and C(8, 2).
To Prove:
The points A, B, and C are collinear using the concept of the equation of a line.
Proof:
Three points are collinear if they lie on the same straight line. We can prove this by finding the equation of the line passing through two of the points and then checking if the third point satisfies that equation.
Let's find the equation of the line passing through points A(3, 0) and B(–2, –2).
First, calculate the slope ($m$) of the line segment AB:
$m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-2 - 0}{-2 - 3} = \frac{-2}{-5} = \frac{2}{5}$
Now, use the point-slope form of the equation of a line, $y - y_1 = m(x - x_1)$, using point A(3, 0) and slope $m = \frac{2}{5}$:
$y - 0 = \frac{2}{5}(x - 3)$
$y = \frac{2}{5}(x - 3)$
Multiply both sides by 5 to eliminate the fraction:
$5y = 2(x - 3)$
$5y = 2x - 6$
Rearrange the equation into the general form $Ax + By + C = 0$:
$2x - 5y - 6 = 0$
This is the equation of the line passing through points A and B.
Now, we need to check if the third point C(8, 2) lies on this line. Substitute the coordinates of C ($x=8, y=2$) into the equation $2x - 5y - 6 = 0$:
Left Hand Side (LHS) = $2(8) - 5(2) - 6$
LHS = $16 - 10 - 6$
LHS = $6 - 6$
LHS = $0$
Right Hand Side (RHS) = 0
Since LHS = RHS, the point C(8, 2) satisfies the equation of the line passing through A and B.
Therefore, the point C lies on the same line as points A and B.
Hence, the three points (3, 0), (– 2, – 2) and (8, 2) are collinear.
Example 13 to 19 (Before Exercise 10.3)
Example 13: Equation of a line is 3x – 4y + 10 = 0. Find its
(i) slope,
(ii) x - and y-intercepts.
Answer:
Given:
The equation of the line is $3x - 4y + 10 = 0$.
To Find:
(i) The slope of the line ($m$).
(ii) The x-intercept and y-intercept of the line.
Solution:
(i) Slope:
To find the slope, we can rearrange the given equation into the slope-intercept form, $y = mx + c$, where $m$ is the slope and $c$ is the y-intercept.
$3x - 4y + 10 = 0$
Keep the y-term on one side:
$-4y = -3x - 10$
Divide both sides by -4:
$y = \frac{-3}{-4}x - \frac{10}{-4}$
$y = \frac{3}{4}x + \frac{10}{4}$
$y = \frac{3}{4}x + \frac{5}{2}$
Comparing this equation with $y = mx + c$, we get:
Slope $m = \frac{3}{4}$.
(ii) Intercepts:
Y-intercept:
From the slope-intercept form $y = \frac{3}{4}x + \frac{5}{2}$, the y-intercept $c$ is $\frac{5}{2}$.
Alternatively, to find the y-intercept, set $x = 0$ in the original equation $3x - 4y + 10 = 0$:
$3(0) - 4y + 10 = 0$
$0 - 4y + 10 = 0$
$-4y = -10$
$y = \frac{-10}{-4} = \frac{5}{2}$
So, the y-intercept is $\frac{5}{2}$.
X-intercept:
To find the x-intercept, set $y = 0$ in the original equation $3x - 4y + 10 = 0$:
$3x - 4(0) + 10 = 0$
$3x - 0 + 10 = 0$
$3x = -10$
$x = -\frac{10}{3}$
So, the x-intercept is $-\frac{10}{3}$.
Summary:
(i) The slope of the line is $\frac{3}{4}$.
(ii) The x-intercept is $-\frac{10}{3}$ and the y-intercept is $\frac{5}{2}$.
Example 14: Reduce the equation $\sqrt{3}$x + y - 8 into normal form. Find the values of p and ω.
Answer:
Given:
The equation of the line is $\sqrt{3}x + y - 8 = 0$.
To Find:
1. The normal form of the equation.
2. The value of $p$ (perpendicular distance from the origin).
3. The value of $\omega$ (angle the normal makes with the positive x-axis).
Solution:
The given equation is:
$\sqrt{3}x + y - 8 = 0$
Rewrite the equation in the form $Ax + By = C$:
$\sqrt{3}x + y = 8$
Here, $A = \sqrt{3}$ and $B = 1$. The constant term $C = 8$ is positive.
The normal form of a line is $x \cos \omega + y \sin \omega = p$, where $p$ is the length of the perpendicular from the origin and must be positive.
To convert the equation $Ax + By = C$ (where $C > 0$) to the normal form, we divide the entire equation by $\sqrt{A^2 + B^2}$.
Calculate $\sqrt{A^2 + B^2}$:
$\sqrt{(\sqrt{3})^2 + (1)^2} = \sqrt{3 + 1} = \sqrt{4} = 2$
Divide the equation $\sqrt{3}x + y = 8$ by 2:
$\frac{\sqrt{3}}{2}x + \frac{1}{2}y = \frac{8}{2}$
$\frac{\sqrt{3}}{2}x + \frac{1}{2}y = 4$
This equation is now in the normal form $x \cos \omega + y \sin \omega = p$.
Comparing the equation $\frac{\sqrt{3}}{2}x + \frac{1}{2}y = 4$ with $x \cos \omega + y \sin \omega = p$, we get:
$\cos \omega = \frac{\sqrt{3}}{2}$
$\sin \omega = \frac{1}{2}$
$p = 4$
Since $\cos \omega$ and $\sin \omega$ are both positive, the angle $\omega$ lies in the first quadrant.
The angle $\omega$ for which $\cos \omega = \frac{\sqrt{3}}{2}$ and $\sin \omega = \frac{1}{2}$ is $30^\circ$ or $\frac{\pi}{6}$ radians.
Final Answer:
The normal form of the equation is $\frac{\sqrt{3}}{2}x + \frac{1}{2}y = 4$.
The value of the perpendicular distance from the origin is $p = 4$.
The angle the normal makes with the positive x-axis is $\omega = 30^\circ$ (or $\frac{\pi}{6}$ radians).
Example 15: Find the angle between the lines y - $\sqrt{3}$x - 5 = 0 and $\sqrt{3}$y - x + 6 = 0.
Answer:
Given:
The equations of the two lines are:
Line 1: $L_1: y - \sqrt{3}x - 5 = 0$
Line 2: $L_2: \sqrt{3}y - x + 6 = 0$
To Find:
The angle between the lines $L_1$ and $L_2$.
Solution:
To find the angle between two lines, we first need to find their slopes.
Slope of Line 1 ($m_1$):
Rearrange the equation $y - \sqrt{3}x - 5 = 0$ into the slope-intercept form $y = mx + c$.
$y = \sqrt{3}x + 5$
Comparing with $y = m_1 x + c_1$, the slope of Line 1 is $m_1 = \sqrt{3}$.
Slope of Line 2 ($m_2$):
Rearrange the equation $\sqrt{3}y - x + 6 = 0$ into the slope-intercept form $y = mx + c$.
$\sqrt{3}y = x - 6$
$y = \frac{1}{\sqrt{3}}x - \frac{6}{\sqrt{3}}$
Comparing with $y = m_2 x + c_2$, the slope of Line 2 is $m_2 = \frac{1}{\sqrt{3}}$.
Let $\theta$ be the acute angle between the lines $L_1$ and $L_2$. The formula for the tangent of the angle between two lines with slopes $m_1$ and $m_2$ is:
$\tan \theta = \left| \frac{m_2 - m_1}{1 + m_1 m_2} \right|$
Substitute the values of $m_1$ and $m_2$:
$m_1 = \sqrt{3}$
$m_2 = \frac{1}{\sqrt{3}}$
$m_2 - m_1 = \frac{1}{\sqrt{3}} - \sqrt{3} = \frac{1 - (\sqrt{3})(\sqrt{3})}{\sqrt{3}} = \frac{1 - 3}{\sqrt{3}} = -\frac{2}{\sqrt{3}}$
$1 + m_1 m_2 = 1 + (\sqrt{3}) \left(\frac{1}{\sqrt{3}}\right) = 1 + 1 = 2$
Now, substitute these values into the formula for $\tan \theta$:
$\tan \theta = \left| \frac{-\frac{2}{\sqrt{3}}}{2} \right| = \left| -\frac{2}{2\sqrt{3}} \right| = \left| -\frac{1}{\sqrt{3}} \right| = \frac{1}{\sqrt{3}}$
Since $\tan \theta = \frac{1}{\sqrt{3}}$, the acute angle $\theta$ is:
$\theta = \arctan\left(\frac{1}{\sqrt{3}}\right) = 30^\circ$ (or $\frac{\pi}{6}$ radians).
The obtuse angle between the lines is $180^\circ - 30^\circ = 150^\circ$. Typically, the angle between lines refers to the acute angle.
Therefore, the angle between the given lines is $30^\circ$.
Example 16: Show that two lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, where b1 , b2 ≠ 0 are:
(i) Parallel if $\frac{a_1}{a_2} = \frac{b_1}{b_2}$, and
(ii) Perpendicular if $a_1 a_2 + b_1 b_2 = 0$.
Answer:
Given:
Two lines $L_1$ and $L_2$ with equations:
$L_1: a_1x + b_1y + c_1 = 0$
$L_2: a_2x + b_2y + c_2 = 0$
It is also given that $b_1 \neq 0$ and $b_2 \neq 0$.
To Prove:
(i) The lines are parallel if $\frac{a_1}{a_2} = \frac{b_1}{b_2}$.
(ii) The lines are perpendicular if $a_1 a_2 + b_1 b_2 = 0$.
Proof:
Since $b_1 \neq 0$ and $b_2 \neq 0$, we can write the equations of the lines in the slope-intercept form ($y = mx + c$) to find their slopes.
Slope of Line 1 ($m_1$):
From $a_1x + b_1y + c_1 = 0$:
$b_1y = -a_1x - c_1$
$y = \left(-\frac{a_1}{b_1}\right)x + \left(-\frac{c_1}{b_1}\right)$
Comparing with $y = m_1x + c'_1$, the slope of Line 1 is $m_1 = -\frac{a_1}{b_1}$.
Slope of Line 2 ($m_2$):
From $a_2x + b_2y + c_2 = 0$:
$b_2y = -a_2x - c_2$
$y = \left(-\frac{a_2}{b_2}\right)x + \left(-\frac{c_2}{b_2}\right)$
Comparing with $y = m_2x + c'_2$, the slope of Line 2 is $m_2 = -\frac{a_2}{b_2}$.
(i) Condition for Parallel Lines:
Two lines are parallel if and only if their slopes are equal, i.e., $m_1 = m_2$.
So, we set the slopes equal:
$-\frac{a_1}{b_1} = -\frac{a_2}{b_2}$
Multiply both sides by -1:
$\frac{a_1}{b_1} = \frac{a_2}{b_2}$
Rearranging the terms (assuming $a_2 \neq 0$ and $b_1 \neq 0$):
$\frac{a_1}{a_2} = \frac{b_1}{b_2}$
Thus, the lines $L_1$ and $L_2$ are parallel if $\frac{a_1}{a_2} = \frac{b_1}{b_2}$.
(ii) Condition for Perpendicular Lines:
Two lines are perpendicular if and only if the product of their slopes is -1, i.e., $m_1 m_2 = -1$.
So, we calculate the product of the slopes:
$m_1 m_2 = \left(-\frac{a_1}{b_1}\right) \left(-\frac{a_2}{b_2}\right)$
$m_1 m_2 = \frac{a_1 a_2}{b_1 b_2}$
Set the product equal to -1:
$\frac{a_1 a_2}{b_1 b_2} = -1$
Multiply both sides by $b_1 b_2$ (which is non-zero since $b_1 \neq 0$ and $b_2 \neq 0$):
$a_1 a_2 = -b_1 b_2$
Rearrange the terms:
$a_1 a_2 + b_1 b_2 = 0$
Thus, the lines $L_1$ and $L_2$ are perpendicular if $a_1 a_2 + b_1 b_2 = 0$.
Hence Proved.
Example 17: Find the equation of a line perpendicular to the line x - 2y + 3 = 0 and passing through the point (1, – 2).
Answer:
Given:
The equation of the given line $L_1$ is $x - 2y + 3 = 0$.
The required line $L_2$ passes through the point $P(1, -2)$.
The required line $L_2$ is perpendicular to the given line $L_1$.
To Find:
The equation of the required line $L_2$.
Solution:
First, find the slope of the given line $L_1: x - 2y + 3 = 0$.
Rewrite the equation in the slope-intercept form ($y = mx + c$):
$-2y = -x - 3$
$y = \frac{-1}{-2}x - \frac{3}{-2}$
$y = \frac{1}{2}x + \frac{3}{2}$
The slope of the given line $L_1$ is $m_1 = \frac{1}{2}$.
Let the slope of the required line $L_2$ be $m_2$.
Since $L_2$ is perpendicular to $L_1$, the product of their slopes must be -1:
$m_1 \times m_2 = -1$
$\left(\frac{1}{2}\right) \times m_2 = -1$
$m_2 = -2$
The required line $L_2$ passes through the point $(x_1, y_1) = (1, -2)$ and has a slope $m_2 = -2$.
Use the point-slope form of the equation of a line: $y - y_1 = m_2(x - x_1)$.
Substitute the values:
$y - (-2) = -2(x - 1)$
$y + 2 = -2(x - 1)$
$y + 2 = -2x + 2$
Rearrange the terms to get the equation in the general form $Ax + By + C = 0$:
$2x + y + 2 - 2 = 0$
$2x + y = 0$
Therefore, the required equation of the line is $2x + y = 0$.
Alternate Method:
The equation of any line perpendicular to $ax + by + c = 0$ is of the form $bx - ay + k = 0$, where k is a constant.
The given line is $x - 2y + 3 = 0$. Here $a=1$, $b=-2$.
So, the equation of a line perpendicular to it is $-2x - 1y + k = 0$, or multiplying by -1, $2x + y - k = 0$. Let $-k = k'$ (another constant).
The equation is $2x + y + k' = 0$.
This line passes through the point (1, -2). Substitute $x=1$ and $y=-2$ into the equation to find $k'$:
$2(1) + (-2) + k' = 0$
$2 - 2 + k' = 0$
$0 + k' = 0$
$k' = 0$
Substitute $k' = 0$ back into the equation $2x + y + k' = 0$:
$2x + y + 0 = 0$
$2x + y = 0$
This confirms the required equation is $2x + y = 0$.
Example 18: Find the distance of the point (3, – 5) from the line 3x – 4y –26 = 0.
Answer:
Given:
The point $P(x_1, y_1) = (3, -5)$.
The equation of the line is $L: 3x - 4y - 26 = 0$.
To Find:
The perpendicular distance from the point P to the line L.
Solution:
The perpendicular distance $d$ from a point $(x_1, y_1)$ to the line $Ax + By + C = 0$ is given by the formula:
$d = \frac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}}$
Comparing the given equation $3x - 4y - 26 = 0$ with $Ax + By + C = 0$, we have:
$A = 3$
$B = -4$
$C = -26$
The coordinates of the point are $(x_1, y_1) = (3, -5)$.
Substitute these values into the distance formula:
$d = \frac{|3(3) + (-4)(-5) + (-26)|}{\sqrt{(3)^2 + (-4)^2}}$
Calculate the numerator:
$|3(3) + (-4)(-5) - 26| = |9 + 20 - 26| = |29 - 26| = |3| = 3$
Calculate the denominator:
$\sqrt{(3)^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5$
Now, find the distance $d$:
$d = \frac{3}{5}$
Therefore, the distance of the point (3, – 5) from the line 3x – 4y – 26 = 0 is $\frac{3}{5}$ units.
Example 19: Find the distance between the parallel lines 3x – 4y + 7 = 0 and 3x – 4y + 5 = 0
Answer:
Given:
The equations of the two parallel lines are:
$L_1: 3x - 4y + 7 = 0$
$L_2: 3x - 4y + 5 = 0$
To Find:
The distance between the parallel lines $L_1$ and $L_2$.
Solution:
The two lines are parallel because their slopes are equal. For $Ax + By + C = 0$, the slope is $-A/B$.
Slope of $L_1 = -3/(-4) = 3/4$.
Slope of $L_2 = -3/(-4) = 3/4$.
The distance $d$ between two parallel lines $Ax + By + C_1 = 0$ and $Ax + By + C_2 = 0$ is given by the formula:
$d = \frac{|C_1 - C_2|}{\sqrt{A^2 + B^2}}$
Comparing the given equations with the standard form:
For $L_1: 3x - 4y + 7 = 0$, we have $A = 3$, $B = -4$, $C_1 = 7$.
For $L_2: 3x - 4y + 5 = 0$, we have $A = 3$, $B = -4$, $C_2 = 5$.
Substitute these values into the distance formula:
$d = \frac{|7 - 5|}{\sqrt{(3)^2 + (-4)^2}}$
Calculate the numerator:
$|7 - 5| = |2| = 2$
Calculate the denominator:
$\sqrt{(3)^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5$
Now, find the distance $d$:
$d = \frac{2}{5}$
Therefore, the distance between the parallel lines 3x – 4y + 7 = 0 and 3x – 4y + 5 = 0 is $\frac{2}{5}$ units.
Exercise 10.3
Question 1. Reduce the following equations into slope - intercept form and find their slopes and the y - intercepts.
(i) x + 7y = 0,
(ii) 6x + 3y – 5 = 0,
(iii) y = 0.
Answer:
The slope-intercept form of a line is $y = mx + c$, where $m$ is the slope and $c$ is the y-intercept.
(i) x + 7y = 0
Given equation: $x + 7y = 0$
Rearrange to isolate the y-term:
$7y = -x$
Divide by 7:
$y = -\frac{1}{7}x$
This can be written as:
$y = \left(-\frac{1}{7}\right)x + 0$
Comparing this with $y = mx + c$, we get:
Slope, $m = -\frac{1}{7}$
Y-intercept, $c = 0$
The slope-intercept form is $y = -\frac{1}{7}x + 0$, the slope is $-\frac{1}{7}$, and the y-intercept is 0.
(ii) 6x + 3y – 5 = 0
Given equation: $6x + 3y - 5 = 0$
Rearrange to isolate the y-term:
$3y = -6x + 5$
Divide by 3:
$y = \frac{-6}{3}x + \frac{5}{3}$
$y = -2x + \frac{5}{3}$
Comparing this with $y = mx + c$, we get:
Slope, $m = -2$
Y-intercept, $c = \frac{5}{3}$
The slope-intercept form is $y = -2x + \frac{5}{3}$, the slope is -2, and the y-intercept is $\frac{5}{3}$.
(iii) y = 0
Given equation: $y = 0$
This equation represents the x-axis.
We can write it in the slope-intercept form $y = mx + c$ as:
$y = 0 \cdot x + 0$
Comparing this with $y = mx + c$, we get:
Slope, $m = 0$
Y-intercept, $c = 0$
The slope-intercept form is $y = 0x + 0$, the slope is 0, and the y-intercept is 0.
Question 2. Reduce the following equations into intercept form and find their intercepts on the axes.
(i) 3x + 2y – 12 = 0,
(ii) 4x – 3y = 6,
(iii) 3y + 2 = 0.
Answer:
The intercept form of a line is $\frac{x}{a} + \frac{y}{b} = 1$, where $a$ is the x-intercept and $b$ is the y-intercept.
(i) 3x + 2y – 12 = 0
Given equation: $3x + 2y - 12 = 0$
Move the constant term to the right side:
$3x + 2y = 12$
Divide both sides by 12 to make the right side equal to 1:
$\frac{3x}{12} + \frac{2y}{12} = \frac{12}{12}$
Simplify the fractions:
$\frac{x}{4} + \frac{y}{6} = 1$
This is the intercept form.
Comparing with $\frac{x}{a} + \frac{y}{b} = 1$, we get:
X-intercept, $a = 4$
Y-intercept, $b = 6$
The intercept form is $\frac{x}{4} + \frac{y}{6} = 1$, the x-intercept is 4, and the y-intercept is 6.
(ii) 4x – 3y = 6
Given equation: $4x - 3y = 6$
Divide both sides by 6 to make the right side equal to 1:
$\frac{4x}{6} - \frac{3y}{6} = \frac{6}{6}$
Simplify the fractions:
$\frac{2x}{3} - \frac{y}{2} = 1$
Rewrite in the standard intercept form $\frac{x}{a} + \frac{y}{b} = 1$:
$\frac{x}{3/2} + \frac{y}{-2} = 1$
This is the intercept form.
Comparing with $\frac{x}{a} + \frac{y}{b} = 1$, we get:
X-intercept, $a = \frac{3}{2}$
Y-intercept, $b = -2$
The intercept form is $\frac{x}{3/2} + \frac{y}{-2} = 1$, the x-intercept is $\frac{3}{2}$, and the y-intercept is -2.
(iii) 3y + 2 = 0
Given equation: $3y + 2 = 0$
Rearrange the equation:
$3y = -2$
$y = -\frac{2}{3}$
This equation represents a horizontal line parallel to the x-axis.
Intercepts:
To find the y-intercept, we look at the equation $y = -\frac{2}{3}$. The line crosses the y-axis at $y = -\frac{2}{3}$. So, the y-intercept is $b = -\frac{2}{3}$.
To find the x-intercept, we need to find the point where the line crosses the x-axis (where $y=0$). Since the equation is $y = -\frac{2}{3}$, $y$ can never be 0. This line is parallel to the x-axis and does not intersect it.
Therefore, there is no x-intercept.
Intercept Form:
The standard intercept form $\frac{x}{a} + \frac{y}{b} = 1$ requires finite non-zero intercepts $a$ and $b$. Since there is no x-intercept (or it can be considered infinite), this equation cannot be reduced to the standard intercept form.
The intercepts are: x-intercept: None, y-intercept: $-\frac{2}{3}$.
Question 3. Reduce the following equations into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.
(i) x – $\sqrt{3}$y + 8 = 0,
(ii) y – 2 = 0,
(iii) x – y = 4.
Answer:
The normal form of a line is $x \cos \omega + y \sin \omega = p$, where $p$ is the positive perpendicular distance from the origin to the line, and $\omega$ is the angle the perpendicular makes with the positive x-axis ($0 \leq \omega < 360^\circ$).
(i) x – $\sqrt{3}$y + 8 = 0
Given equation: $x - \sqrt{3}y + 8 = 0$
Rewrite as $x - \sqrt{3}y = -8$.
Since the constant term on the right side must be positive for the normal form ($p>0$), multiply the equation by -1:
$-x + \sqrt{3}y = 8$
Comparing with $Ax + By = C$, we have $A = -1$, $B = \sqrt{3}$, $C = 8$.
Calculate $\sqrt{A^2 + B^2}$:
$\sqrt{(-1)^2 + (\sqrt{3})^2} = \sqrt{1 + 3} = \sqrt{4} = 2$
Divide the equation $-x + \sqrt{3}y = 8$ by 2:
$\frac{-1}{2}x + \frac{\sqrt{3}}{2}y = \frac{8}{2}$
$-\frac{1}{2}x + \frac{\sqrt{3}}{2}y = 4$
This is the normal form. Comparing with $x \cos \omega + y \sin \omega = p$:
$\cos \omega = -\frac{1}{2}$
$\sin \omega = \frac{\sqrt{3}}{2}$
$p = 4$
Since $\cos \omega$ is negative and $\sin \omega$ is positive, $\omega$ lies in the second quadrant.
The angle $\omega = 120^\circ$ (or $\frac{2\pi}{3}$ radians).
Normal form: $-\frac{1}{2}x + \frac{\sqrt{3}}{2}y = 4$
Perpendicular distance from origin, $p = 4$.
Angle $\omega = 120^\circ$.
(ii) y – 2 = 0
Given equation: $y - 2 = 0$
Rewrite as $y = 2$.
In the form $Ax + By = C$: $0x + 1y = 2$.
Here $A = 0$, $B = 1$, $C = 2$.
Calculate $\sqrt{A^2 + B^2}$:
$\sqrt{0^2 + 1^2} = \sqrt{1} = 1$
Divide the equation $0x + 1y = 2$ by 1:
$0x + 1y = 2$
This is the normal form. Comparing with $x \cos \omega + y \sin \omega = p$:
$\cos \omega = 0$
$\sin \omega = 1$
$p = 2$
The angle $\omega$ for which $\cos \omega = 0$ and $\sin \omega = 1$ is $\omega = 90^\circ$ (or $\frac{\pi}{2}$ radians).
Normal form: $0x + 1y = 2$ (or simply $y=2$)
Perpendicular distance from origin, $p = 2$.
Angle $\omega = 90^\circ$.
(iii) x – y = 4
Given equation: $x - y = 4$
This is in the form $Ax + By = C$ with $C=4$ positive.
Here $A = 1$, $B = -1$, $C = 4$.
Calculate $\sqrt{A^2 + B^2}$:
$\sqrt{1^2 + (-1)^2} = \sqrt{1 + 1} = \sqrt{2}$
Divide the equation $x - y = 4$ by $\sqrt{2}$:
$\frac{1}{\sqrt{2}}x - \frac{1}{\sqrt{2}}y = \frac{4}{\sqrt{2}}$
Rationalize the right side: $\frac{4}{\sqrt{2}} = \frac{4\sqrt{2}}{2} = 2\sqrt{2}$.
$\frac{1}{\sqrt{2}}x - \frac{1}{\sqrt{2}}y = 2\sqrt{2}$
This is the normal form. Comparing with $x \cos \omega + y \sin \omega = p$:
$\cos \omega = \frac{1}{\sqrt{2}}$
$\sin \omega = -\frac{1}{\sqrt{2}}$
$p = 2\sqrt{2}$
Since $\cos \omega$ is positive and $\sin \omega$ is negative, $\omega$ lies in the fourth quadrant.
The angle $\omega = 315^\circ$ (or $\frac{7\pi}{4}$ radians).
Normal form: $\frac{1}{\sqrt{2}}x - \frac{1}{\sqrt{2}}y = 2\sqrt{2}$
Perpendicular distance from origin, $p = 2\sqrt{2}$.
Angle $\omega = 315^\circ$.
Question 4. Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).
Answer:
Given:
The point is P(–1, 1).
The equation of the line is $12(x + 6) = 5(y – 2)$.
To Find:
The distance of the point P from the given line.
Solution:
First, let's convert the equation of the line to the standard form $Ax + By + C = 0$.
$12(x + 6) = 5(y – 2)$
$12x + 72 = 5y – 10$
$12x – 5y + 72 + 10 = 0$
$12x – 5y + 82 = 0$
Comparing this equation with the standard form $Ax + By + C = 0$, we get:
$A = 12$, $B = –5$, and $C = 82$.
The given point is $(x₁, y₁) = (–1, 1)$.
The formula for the perpendicular distance 'd' of a point $(x₁, y₁)$ from the line $Ax + By + C = 0$ is:
$d = \frac{|Ax₁ + By₁ + C|}{\sqrt{A² + B²}}$
Substituting the values:
$d = \frac{|12(–1) + (–5)(1) + 82|}{\sqrt{(12)² + (–5)²}}$
$d = \frac{|–12 – 5 + 82|}{\sqrt{144 + 25}}$
$d = \frac{|65|}{\sqrt{169}}$
$d = \frac{65}{13}$
$d = 5$
Therefore, the distance of the point (–1, 1) from the line $12(x + 6) = 5(y – 2)$ is 5 units.
Question 5. Find the points on the x-axis, whose distances from the line $\frac{x}{3}$ + $\frac{y}{4}$ = 1 are 4 units.
Answer:
Given:
The equation of the line is $\frac{x}{3} + \frac{y}{4} = 1$.
The required distance from the line is 4 units.
The points lie on the x-axis.
To Find:
The coordinates of the points on the x-axis satisfying the given condition.
Solution:
First, convert the equation of the line to the standard form $Ax + By + C = 0$.
$\frac{x}{3} + \frac{y}{4} = 1$
Taking the LCM of the denominators (3 and 4), which is 12:
$12 \left( \frac{x}{3} \right) + 12 \left( \frac{y}{4} \right) = 12(1)$
$4x + 3y = 12$
$4x + 3y - 12 = 0$
Comparing this with $Ax + By + C = 0$, we have $A = 4$, $B = 3$, and $C = -12$.
Let a point on the x-axis be $P(x₁, 0)$.
The distance 'd' of a point $(x₁, y₁)$ from the line $Ax + By + C = 0$ is given by the formula:
$d = \frac{|Ax₁ + By₁ + C|}{\sqrt{A² + B²}}$
We are given that the distance $d = 4$ units.
Substituting the values of $A$, $B$, $C$, $(x₁, y₁) = (x₁, 0)$, and $d=4$ into the formula:
$4 = \frac{|4(x₁) + 3(0) - 12|}{\sqrt{(4)² + (3)²}}$
$4 = \frac{|4x₁ - 12|}{\sqrt{16 + 9}}$
$4 = \frac{|4x₁ - 12|}{\sqrt{25}}$
$4 = \frac{|4x₁ - 12|}{5}$
Multiply both sides by 5:
$4 \times 5 = |4x₁ - 12|$
$20 = |4x₁ - 12|$
This gives two possibilities:
Case 1: $4x₁ - 12 = 20$
$4x₁ = 20 + 12$
$4x₁ = 32$
$x₁ = \frac{32}{4}$
$x₁ = 8$
So, one point is (8, 0).
Case 2: $4x₁ - 12 = -20$
$4x₁ = -20 + 12$
$4x₁ = -8$
$x₁ = \frac{-8}{4}$
$x₁ = -2$
So, the other point is (–2, 0).
Therefore, the points on the x-axis whose distances from the line $\frac{x}{3} + \frac{y}{4} = 1$ are 4 units are (8, 0) and (–2, 0).
Question 6. Find the distance between parallel lines
(i) 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0
(ii) l (x + y) + p = 0 and l (x + y) – r = 0.
Answer:
Solution (i):
The given parallel lines are:
$15x + 8y – 34 = 0$ ...(1)
$15x + 8y + 31 = 0$ ...(2)
These lines are of the form $Ax + By + C₁ = 0$ and $Ax + By + C₂ = 0$.
Comparing equation (1) and (2) with the standard form, we get:
$A = 15$, $B = 8$, $C₁ = -34$, and $C₂ = 31$.
The distance 'd' between two parallel lines $Ax + By + C₁ = 0$ and $Ax + By + C₂ = 0$ is given by the formula:
$d = \frac{|C₁ - C₂|}{\sqrt{A² + B²}}$
Substituting the values:
$d = \frac{|-34 - 31|}{\sqrt{(15)² + (8)²}}$
$d = \frac{|-65|}{\sqrt{225 + 64}}$
$d = \frac{65}{\sqrt{289}}$
$d = \frac{65}{17}$
Therefore, the distance between the lines $15x + 8y – 34 = 0$ and $15x + 8y + 31 = 0$ is $\frac{65}{17}$ units.
Solution (ii):
The given parallel lines are:
$l(x + y) + p = 0 \implies lx + ly + p = 0$ ...(3)
$l(x + y) – r = 0 \implies lx + ly – r = 0$ ...(4)
These lines are of the form $Ax + By + C₁ = 0$ and $Ax + By + C₂ = 0$.
Comparing equation (3) and (4) with the standard form, we get:
$A = l$, $B = l$, $C₁ = p$, and $C₂ = -r$.
The distance 'd' between two parallel lines $Ax + By + C₁ = 0$ and $Ax + By + C₂ = 0$ is given by the formula:
$d = \frac{|C₁ - C₂|}{\sqrt{A² + B²}}$
Substituting the values:
$d = \frac{|p - (-r)|}{\sqrt{(l)² + (l)²}}$
$d = \frac{|p + r|}{\sqrt{l² + l²}}$
$d = \frac{|p + r|}{\sqrt{2l²}}$
$d = \frac{|p + r|}{\sqrt{2} \sqrt{l²}}$
$d = \frac{|p + r|}{\sqrt{2} |l|}$
Therefore, the distance between the lines $l(x + y) + p = 0$ and $l(x + y) – r = 0$ is $\frac{|p + r|}{\sqrt{2}|l|}$ units (assuming $l \neq 0$).
Question 7. Find equation of the line parallel to the line 3x - 4y + 2 = 0 and passing through the point (–2, 3).
Answer:
Given:
The equation of the given line is $3x - 4y + 2 = 0$.
The point through which the required line passes is $(-2, 3)$.
To Find:
The equation of the line parallel to the given line and passing through the given point.
Solution:
First, find the slope of the given line $3x - 4y + 2 = 0$.
We can rewrite the equation in the slope-intercept form ($y = mx + c$):
$-4y = -3x - 2$
$4y = 3x + 2$
$y = \frac{3}{4}x + \frac{2}{4}$
$y = \frac{3}{4}x + \frac{1}{2}$
The slope ($m$) of the given line is $\frac{3}{4}$.
Since the required line is parallel to the given line, it must have the same slope.
So, the slope of the required line is $m = \frac{3}{4}$.
The required line passes through the point $(x₁, y₁) = (-2, 3)$.
Using the point-slope form of a line, $y - y₁ = m(x - x₁)$:
$y - 3 = \frac{3}{4}(x - (-2))$
$y - 3 = \frac{3}{4}(x + 2)$
Multiply both sides by 4 to eliminate the fraction:
$4(y - 3) = 3(x + 2)$
$4y - 12 = 3x + 6$
Rearrange the terms into the standard form $Ax + By + C = 0$:
$0 = 3x - 4y + 6 + 12$
$3x - 4y + 18 = 0$
Alternate Solution:
The equation of any line parallel to $Ax + By + C = 0$ is of the form $Ax + By + k = 0$, where $k$ is a constant.
The given line is $3x - 4y + 2 = 0$.
So, the equation of a line parallel to it is $3x - 4y + k = 0$.
Since this line passes through the point $(-2, 3)$, substitute $x = -2$ and $y = 3$ into the equation:
$3(-2) - 4(3) + k = 0$
$-6 - 12 + k = 0$
$-18 + k = 0$
$k = 18$
Substitute the value of $k = 18$ back into the equation of the parallel line:
$3x - 4y + 18 = 0$
Therefore, the equation of the required line is $3x - 4y + 18 = 0$.
Question 8. Find equation of the line perpendicular to the line x – 7y + 5 = 0 and having x intercept 3.
Answer:
Given:
The equation of the given line is $x - 7y + 5 = 0$.
The required line is perpendicular to the given line.
The x-intercept of the required line is 3.
To Find:
The equation of the required line.
Solution:
First, find the slope of the given line $x - 7y + 5 = 0$.
We can rewrite the equation in the slope-intercept form ($y = mx + c$):
$-7y = -x - 5$
$7y = x + 5$
$y = \frac{1}{7}x + \frac{5}{7}$
The slope ($m₁$) of the given line is $\frac{1}{7}$.
Let the slope of the required line be $m₂$.
Since the required line is perpendicular to the given line, the product of their slopes is -1.
$m₁ \times m₂ = -1$
$\frac{1}{7} \times m₂ = -1$
$m₂ = -7$
The required line has an x-intercept of 3. This means the line passes through the point where the y-coordinate is 0 and the x-coordinate is 3. So, the line passes through the point $(x₁, y₁) = (3, 0)$.
Using the point-slope form of a line, $y - y₁ = m₂(x - x₁)$:
$y - 0 = -7(x - 3)$
$y = -7x + 21$
Rearrange the terms into the standard form $Ax + By + C = 0$:
$7x + y - 21 = 0$
Alternate Solution:
The equation of the given line is $x - 7y + 5 = 0$.
The equation of any line perpendicular to $Ax + By + C = 0$ is of the form $Bx - Ay + k = 0$, where $k$ is a constant.
Here, $A = 1$ and $B = -7$.
So, the equation of a line perpendicular to the given line is:
$-7x - (1)y + k = 0$
$-7x - y + k = 0$
Multiplying by -1 (optional, but makes the x-coefficient positive):
$7x + y - k = 0$. Let $k' = -k$.
$7x + y + k' = 0$.
The line has an x-intercept of 3, which means it passes through the point (3, 0).
Substitute $x = 3$ and $y = 0$ into the equation $7x + y + k' = 0$:
$7(3) + (0) + k' = 0$
$21 + 0 + k' = 0$
$k' = -21$
Substitute the value of $k' = -21$ back into the equation of the perpendicular line:
$7x + y - 21 = 0$
Therefore, the equation of the required line is $7x + y - 21 = 0$.
Question 9. Find angles between the lines $\sqrt{3}$x + y = 0 and x + $\sqrt{3}$y = 1.
Answer:
Given:
The equations of the two lines are:
Line 1: $\sqrt{3}x + y = 0$
Line 2: $x + \sqrt{3}y = 1$
To Find:
The angles between the given lines.
Solution:
First, find the slopes of the given lines by converting them to the slope-intercept form $y = mx + c$.
For Line 1: $\sqrt{3}x + y = 0$
$y = -\sqrt{3}x + 0$
Comparing with $y = m₁x + c₁$, the slope of the first line is $m₁ = -\sqrt{3}$.
For Line 2: $x + \sqrt{3}y = 1$
$\sqrt{3}y = -x + 1$
$y = -\frac{1}{\sqrt{3}}x + \frac{1}{\sqrt{3}}$
Comparing with $y = m₂x + c₂$, the slope of the second line is $m₂ = -\frac{1}{\sqrt{3}}$.
Let $\theta$ be the acute angle between the two lines. The formula for the tangent of the angle between two lines with slopes $m₁$ and $m₂$ is:
$\tan \theta = \left| \frac{m₂ - m₁}{1 + m₁m₂} \right|$
Substitute the values of $m₁$ and $m₂$:
$\tan \theta = \left| \frac{-\frac{1}{\sqrt{3}} - (-\sqrt{3})}{1 + (-\sqrt{3})\left(-\frac{1}{\sqrt{3}}\right)} \right|$
$\tan \theta = \left| \frac{-\frac{1}{\sqrt{3}} + \sqrt{3}}{1 + 1} \right|$
$\tan \theta = \left| \frac{\frac{-1 + (\sqrt{3} \times \sqrt{3})}{\sqrt{3}}}{2} \right|$
$\tan \theta = \left| \frac{\frac{-1 + 3}{\sqrt{3}}}{2} \right|$
$\tan \theta = \left| \frac{\frac{2}{\sqrt{3}}}{2} \right|$
$\tan \theta = \left| \frac{2}{2\sqrt{3}} \right|$
$\tan \theta = \left| \frac{1}{\sqrt{3}} \right|$
$\tan \theta = \frac{1}{\sqrt{3}}$
Since $\tan \theta = \frac{1}{\sqrt{3}}$, the acute angle $\theta$ is $30^\circ$.
The other angle between the lines is the obtuse angle, which is $180^\circ - \theta$.
$180^\circ - 30^\circ = 150^\circ$.
Therefore, the angles between the lines $\sqrt{3}x + y = 0$ and $x + \sqrt{3}y = 1$ are $30^\circ$ and $150^\circ$.
Question 10. The line through the points (h, 3) and (4, 1) intersects the line 7x - 9y - 19 = 0 at right angle. Find the value of h.
Answer:
Given:
Line 1 passes through the points P(h, 3) and Q(4, 1).
Line 2 has the equation $7x - 9y - 19 = 0$.
Line 1 and Line 2 intersect at a right angle (are perpendicular).
To Find:
The value of h.
Solution:
First, let's find the slope of Line 1, which passes through the points $(h, 3)$ and $(4, 1)$.
Let the slope of Line 1 be $m₁$.
$m₁ = \frac{\text{change in y}}{\text{change in x}} = \frac{1 - 3}{4 - h} = \frac{-2}{4 - h}$.
Next, let's find the slope of Line 2, whose equation is $7x - 9y - 19 = 0$.
We can rewrite this equation in the slope-intercept form ($y = mx + c$):
$-9y = -7x + 19$
$9y = 7x - 19$
$y = \frac{7}{9}x - \frac{19}{9}$
The slope of Line 2 ($m₂$) is $\frac{7}{9}$.
Since the two lines intersect at a right angle, they are perpendicular. The condition for two lines to be perpendicular is that the product of their slopes is -1.
$m₁ \times m₂ = -1$
Substitute the values of $m₁$ and $m₂$:
$\left( \frac{-2}{4 - h} \right) \times \left( \frac{7}{9} \right) = -1$
$\frac{-14}{9(4 - h)} = -1$
$\frac{-14}{36 - 9h} = -1$
Multiply both sides by $-(36 - 9h)$:
$14 = 1 \times (36 - 9h)$
$14 = 36 - 9h$
Rearrange the equation to solve for h:
$9h = 36 - 14$
$9h = 22$
$h = \frac{22}{9}$
Therefore, the value of h is $\frac{22}{9}$.
Question 11. Prove that the line through the point (x1 , y1 ) and parallel to the line Ax + By + C = 0 is
A (x – x1) + B (y – y1) = 0.
Answer:
Given:
A point $P(x₁, y₁)$.
The equation of a line $L₁: Ax + By + C = 0$.
A line $L₂$ passes through the point $P(x₁, y₁)$ and is parallel to the line $L₁$.
To Prove:
The equation of the line $L₂$ is $A(x - x₁) + B(y - y₁) = 0$.
Proof:
First, let's find the slope of the given line $L₁: Ax + By + C = 0$.
Case 1: Assume $B \neq 0$.
We can rewrite the equation in the slope-intercept form ($y = mx + c$):
$By = -Ax - C$
$y = \left(-\frac{A}{B}\right)x + \left(-\frac{C}{B}\right)$
The slope of the line $L₁$ is $m₁ = -\frac{A}{B}$.
Since the required line $L₂$ is parallel to $L₁$, its slope ($m₂$) must be equal to the slope of $L₁$.
$m₂ = m₁ = -\frac{A}{B}$.
The line $L₂$ passes through the point $(x₁, y₁)$.
Using the point-slope form of a line, $y - y₁ = m₂(x - x₁)$:
$y - y₁ = \left(-\frac{A}{B}\right)(x - x₁)$
Multiply both sides by B:
$B(y - y₁) = -A(x - x₁)$
Rearrange the terms:
$A(x - x₁) + B(y - y₁) = 0$
Case 2: Assume $B = 0$.
If $B = 0$, the equation of line $L₁$ becomes $Ax + C = 0$ (assuming $A \neq 0$, otherwise it's not a line).
$Ax = -C$
$x = -\frac{C}{A}$
This is the equation of a vertical line.
A line $L₂$ parallel to a vertical line $L₁$ must also be a vertical line.
Since $L₂$ passes through the point $(x₁, y₁)$, its equation must be $x = x₁$, or $x - x₁ = 0$.
Now let's check the equation we need to prove: $A(x - x₁) + B(y - y₁) = 0$.
Substitute $B = 0$ into this equation:
$A(x - x₁) + 0(y - y₁) = 0$
$A(x - x₁) = 0$
Since $A \neq 0$, we must have $x - x₁ = 0$, which is the same equation we found for the vertical line $L₂$.
In both cases ($B \neq 0$ and $B = 0$), the equation of the line through $(x₁, y₁)$ and parallel to $Ax + By + C = 0$ is $A(x - x₁) + B(y - y₁) = 0$.
Alternate Proof:
The equation of any line parallel to $Ax + By + C = 0$ can be written in the form:
$Ax + By + k = 0$ ...(i)
where k is a constant.
Since this line passes through the point $(x₁, y₁)$, the coordinates of this point must satisfy the equation (i).
Substituting $x = x₁$ and $y = y₁$ into equation (i):
$Ax₁ + By₁ + k = 0$
Solving for k:
$k = -Ax₁ - By₁$
Now, substitute this value of k back into equation (i):
$Ax + By + (-Ax₁ - By₁) = 0$
$Ax + By - Ax₁ - By₁ = 0$
Rearrange the terms by grouping terms with A and B:
$(Ax - Ax₁) + (By - By₁) = 0$
$A(x - x₁) + B(y - y₁) = 0$
Hence, the equation of the required line is $A(x - x₁) + B(y - y₁) = 0$.
Proved.
Question 12. Two lines passing through the point (2, 3) intersects each other at an angle of 60°. If slope of one line is 2, find equation of the other line.
Answer:
Given:
Two lines intersect at the point $P(2, 3)$.
The angle $\theta$ between the two lines is $60^\circ$.
The slope of one line ($L₁$) is $m₁ = 2$.
To Find:
The equation of the other line ($L₂$).
Solution:
Let the slope of the other line ($L₂$) be $m₂$.
The formula for the tangent of the angle $\theta$ between two lines with slopes $m₁$ and $m₂$ is:
$\tan \theta = \left| \frac{m₂ - m₁}{1 + m₁m₂} \right|$
We are given $\theta = 60^\circ$ and $m₁ = 2$. We know that $\tan 60^\circ = \sqrt{3}$.
Substituting the values:
$\sqrt{3} = \left| \frac{m₂ - 2}{1 + 2m₂} \right|$
This absolute value equation leads to two possible cases:
Case 1: $\frac{m₂ - 2}{1 + 2m₂} = \sqrt{3}$
$m₂ - 2 = \sqrt{3}(1 + 2m₂)$
$m₂ - 2 = \sqrt{3} + 2\sqrt{3}m₂$
$m₂ - 2\sqrt{3}m₂ = 2 + \sqrt{3}$
$m₂(1 - 2\sqrt{3}) = 2 + \sqrt{3}$
$m₂ = \frac{2 + \sqrt{3}}{1 - 2\sqrt{3}}$
Rationalizing the denominator:
$m₂ = \frac{2 + \sqrt{3}}{1 - 2\sqrt{3}} \times \frac{1 + 2\sqrt{3}}{1 + 2\sqrt{3}} = \frac{2 + 4\sqrt{3} + \sqrt{3} + 6}{1 - (2\sqrt{3})^2} = \frac{8 + 5\sqrt{3}}{1 - 12} = \frac{8 + 5\sqrt{3}}{-11} = -\frac{8 + 5\sqrt{3}}{11}$
Case 2: $\frac{m₂ - 2}{1 + 2m₂} = -\sqrt{3}$
$m₂ - 2 = -\sqrt{3}(1 + 2m₂)$
$m₂ - 2 = -\sqrt{3} - 2\sqrt{3}m₂$
$m₂ + 2\sqrt{3}m₂ = 2 - \sqrt{3}$
$m₂(1 + 2\sqrt{3}) = 2 - \sqrt{3}$
$m₂ = \frac{2 - \sqrt{3}}{1 + 2\sqrt{3}}$
Rationalizing the denominator:
$m₂ = \frac{2 - \sqrt{3}}{1 + 2\sqrt{3}} \times \frac{1 - 2\sqrt{3}}{1 - 2\sqrt{3}} = \frac{2 - 4\sqrt{3} - \sqrt{3} + 6}{1 - (2\sqrt{3})^2} = \frac{8 - 5\sqrt{3}}{1 - 12} = \frac{8 - 5\sqrt{3}}{-11} = \frac{5\sqrt{3} - 8}{11}$
Now, we find the equation of the line for each slope using the point-slope form $y - y₁ = m(x - x₁)$, with the point $(x₁, y₁) = (2, 3)$.
Equation for Case 1 ($m₂ = -\frac{8 + 5\sqrt{3}}{11}$):
$y - 3 = \left(-\frac{8 + 5\sqrt{3}}{11}\right)(x - 2)$
$11(y - 3) = -(8 + 5\sqrt{3})(x - 2)$
$11y - 33 = -(8 + 5\sqrt{3})x + 2(8 + 5\sqrt{3})$
$11y - 33 = -(8 + 5\sqrt{3})x + 16 + 10\sqrt{3}$
$(8 + 5\sqrt{3})x + 11y - 33 - 16 - 10\sqrt{3} = 0$
$(8 + 5\sqrt{3})x + 11y - (49 + 10\sqrt{3}) = 0$
Equation for Case 2 ($m₂ = \frac{5\sqrt{3} - 8}{11}$):
$y - 3 = \left(\frac{5\sqrt{3} - 8}{11}\right)(x - 2)$
$11(y - 3) = (5\sqrt{3} - 8)(x - 2)$
$11y - 33 = (5\sqrt{3} - 8)x - 2(5\sqrt{3} - 8)$
$11y - 33 = (5\sqrt{3} - 8)x - 10\sqrt{3} + 16$
$(5\sqrt{3} - 8)x - 11y + 33 + 16 - 10\sqrt{3} = 0$
$(5\sqrt{3} - 8)x - 11y + (49 - 10\sqrt{3}) = 0$
Therefore, there are two possible equations for the other line:
$(8 + 5\sqrt{3})x + 11y - (49 + 10\sqrt{3}) = 0$
or
$(5\sqrt{3} - 8)x - 11y + (49 - 10\sqrt{3}) = 0$
(Note: Multiplying the second equation by -1 gives $(8 - 5\sqrt{3})x + 11y - (49 - 10\sqrt{3}) = 0$)
Question 13. Find the equation of the right bisector of the line segment joining the points (3, 4) and (–1, 2).
Answer:
Given:
The endpoints of the line segment are A(3, 4) and B(–1, 2).
To Find:
The equation of the right bisector of the line segment AB.
Solution:
The right bisector of a line segment is a line that is perpendicular to the segment and passes through its midpoint.
Step 1: Find the midpoint of the line segment AB.
Let M be the midpoint of AB. The coordinates of the midpoint M are given by the midpoint formula:
$M = \left( \frac{x₁ + x₂}{2}, \frac{y₁ + y₂}{2} \right)$
Substituting the coordinates of A(3, 4) and B(–1, 2):
$M = \left( \frac{3 + (-1)}{2}, \frac{4 + 2}{2} \right)$
$M = \left( \frac{2}{2}, \frac{6}{2} \right)$
$M = (1, 3)$
So, the right bisector passes through the point (1, 3).
Step 2: Find the slope of the line segment AB.
The slope ($m_{AB}$) of the line segment joining $(x₁, y₁)$ and $(x₂, y₂)$ is given by:
$m_{AB} = \frac{y₂ - y₁}{x₂ - x₁}$
$m_{AB} = \frac{2 - 4}{-1 - 3}$
$m_{AB} = \frac{-2}{-4}$
$m_{AB} = \frac{1}{2}$
Step 3: Find the slope of the right bisector.
Let the slope of the right bisector be $m_{\perp}$. Since the right bisector is perpendicular to the line segment AB, the product of their slopes is -1.
$m_{AB} \times m_{\perp} = -1$
$\frac{1}{2} \times m_{\perp} = -1$
$m_{\perp} = -2$
Step 4: Find the equation of the right bisector.
The right bisector passes through the midpoint M(1, 3) and has a slope $m_{\perp} = -2$.
Using the point-slope form of a line, $y - y₁ = m(x - x₁)$:
$y - 3 = -2(x - 1)$
$y - 3 = -2x + 2$
Rearrange the terms into the standard form $Ax + By + C = 0$:
$2x + y - 3 - 2 = 0$
$2x + y - 5 = 0$
Therefore, the equation of the right bisector of the line segment joining the points (3, 4) and (–1, 2) is $2x + y - 5 = 0$.
Question 14. Find the coordinates of the foot of perpendicular from the point (–1, 3) to the line 3x – 4y – 16 = 0.
Answer:
Given:
The point P(–1, 3).
The equation of the line L is $3x – 4y – 16 = 0$.
To Find:
The coordinates of the foot of the perpendicular from point P to the line L.
Solution:
Let M(h, k) be the coordinates of the foot of the perpendicular from the point P(–1, 3) to the line $3x – 4y – 16 = 0$.
Since M(h, k) lies on the line $3x – 4y – 16 = 0$, its coordinates must satisfy the equation:
$3h – 4k – 16 = 0$
$3h – 4k = 16$
... (i)
Now, let's find the slope of the given line L.
$3x – 4y – 16 = 0$
$-4y = -3x + 16$
$4y = 3x - 16$
$y = \frac{3}{4}x - 4$
The slope of the line L is $m_L = \frac{3}{4}$.
The line segment PM joins P(–1, 3) and M(h, k). Its slope is:
$m_{PM} = \frac{k - 3}{h - (-1)} = \frac{k - 3}{h + 1}$
Since the line segment PM is perpendicular to the line L, the product of their slopes must be -1.
$m_L \times m_{PM} = -1$
$\frac{3}{4} \times \frac{k - 3}{h + 1} = -1$
$3(k - 3) = -4(h + 1)$
$3k - 9 = -4h - 4$
$4h + 3k = 9 - 4$
$4h + 3k = 5$
... (ii)
Now, we need to solve the linear equations (i) and (ii) for h and k.
Multiply equation (i) by 3 and equation (ii) by 4:
$3 \times (3h - 4k = 16) \implies 9h - 12k = 48$ ...(iii)
$4 \times (4h + 3k = 5) \implies 16h + 12k = 20$ ...(iv)
Add equations (iii) and (iv):
$(9h - 12k) + (16h + 12k) = 48 + 20$
$25h = 68$
$h = \frac{68}{25}$
Substitute the value of h into equation (ii):
$4\left(\frac{68}{25}\right) + 3k = 5$
$\frac{272}{25} + 3k = 5$
$3k = 5 - \frac{272}{25}$
$3k = \frac{125 - 272}{25}$
$3k = -\frac{147}{25}$
$k = \frac{-147}{25 \times 3}$
$k = -\frac{49}{25}$
Therefore, the coordinates of the foot of the perpendicular are $\left( \frac{68}{25}, -\frac{49}{25} \right)$.
Question 15. The perpendicular from the origin to the line y = mx + c meets it at the point (–1, 2). Find the values of m and c.
Answer:
Given:
The equation of the line is $L: y = mx + c$.
The perpendicular from the origin O(0, 0) to the line L meets it at the point P(–1, 2).
To Find:
The values of m and c.
Solution:
Since the point P(–1, 2) lies on the line $y = mx + c$, its coordinates must satisfy the equation:
$2 = m(–1) + c$
$2 = -m + c$
$c = m + 2$
... (i)
The slope of the given line $L$ is $m_L = m$.
The line segment OP joins the origin O(0, 0) and the point P(–1, 2). The slope of OP is:
$m_{OP} = \frac{y₂ - y₁}{x₂ - x₁} = \frac{2 - 0}{-1 - 0} = \frac{2}{-1} = -2$.
We are given that the line segment OP (the perpendicular from the origin) is perpendicular to the line L ($y = mx + c$).
The condition for two lines to be perpendicular is that the product of their slopes is -1.
$m_L \times m_{OP} = -1$
$m \times (-2) = -1$
$-2m = -1$
$m = \frac{-1}{-2}$
$m = \frac{1}{2}$
Now, substitute the value of $m = \frac{1}{2}$ into equation (i) to find c:
$c = m + 2$
$c = \frac{1}{2} + 2$
$c = \frac{1}{2} + \frac{4}{2}$
$c = \frac{1 + 4}{2}$
$c = \frac{5}{2}$
Therefore, the values of m and c are:
$m = \frac{1}{2}$ and $c = \frac{5}{2}$.
Question 16. If p and q are the lengths of perpendiculars from the origin to the lines x cos θ - y sin θ = k cos 2θ and x sec θ + y cosec θ = k, respectively, prove that p2 + 4q2 = k2 .
Answer:
Given:
Line 1: $x \cos \theta - y \sin \theta = k \cos 2\theta$
Line 2: $x \sec \theta + y \text{cosec} \theta = k$
$p$ is the length of the perpendicular from the origin (0, 0) to Line 1.
$q$ is the length of the perpendicular from the origin (0, 0) to Line 2.
To Prove:
$p^2 + 4q^2 = k^2$
Proof:
The distance 'd' of a point $(x₁, y₁)$ from the line $Ax + By + C = 0$ is given by the formula:
$d = \frac{|Ax₁ + By₁ + C|}{\sqrt{A² + B²}}$
The point here is the origin $(x₁, y₁) = (0, 0)$.
Calculating p:
Rewrite Line 1 in the standard form $Ax + By + C = 0$:
$x \cos \theta - y \sin \theta - k \cos 2\theta = 0$
Here, $A = \cos \theta$, $B = -\sin \theta$, $C = -k \cos 2\theta$.
The length of the perpendicular $p$ from the origin (0, 0) is:
$p = \frac{|(\cos \theta)(0) + (-\sin \theta)(0) - k \cos 2\theta|}{\sqrt{(\cos \theta)² + (-\sin \theta)²}}$
$p = \frac{|-k \cos 2\theta|}{\sqrt{\cos²\theta + \sin²\theta}}$
Using the identity $\sin²\theta + \cos²\theta = 1$:
$p = \frac{|-k \cos 2\theta|}{\sqrt{1}}$
$p = |-k \cos 2\theta| = |k \cos 2\theta|$
Squaring both sides:
$p^2 = k^2 \cos^2 2\theta$
... (i)
Calculating q:
Rewrite Line 2 in terms of sin and cos:
$x \sec \theta + y \text{cosec} \theta = k$
$\frac{x}{\cos \theta} + \frac{y}{\sin \theta} = k$
Multiply by $\sin \theta \cos \theta$ to clear denominators:
$x \sin \theta + y \cos \theta = k \sin \theta \cos \theta$
Rewrite in the standard form $Ax + By + C = 0$:
$x \sin \theta + y \cos \theta - k \sin \theta \cos \theta = 0$
Here, $A = \sin \theta$, $B = \cos \theta$, $C = -k \sin \theta \cos \theta$.
The length of the perpendicular $q$ from the origin (0, 0) is:
$q = \frac{|(\sin \theta)(0) + (\cos \theta)(0) - k \sin \theta \cos \theta|}{\sqrt{(\sin \theta)² + (\cos \theta)²}}$
$q = \frac{|-k \sin \theta \cos \theta|}{\sqrt{\sin²\theta + \cos²\theta}}$
$q = \frac{|-k \sin \theta \cos \theta|}{\sqrt{1}}$
$q = |-k \sin \theta \cos \theta| = |k \sin \theta \cos \theta|$
Using the double angle identity $\sin 2\theta = 2 \sin \theta \cos \theta$, we have $\sin \theta \cos \theta = \frac{1}{2} \sin 2\theta$.
$q = \left| k \left( \frac{1}{2} \sin 2\theta \right) \right| = \left| \frac{k}{2} \sin 2\theta \right|$
Squaring both sides:
$q^2 = \left( \frac{k}{2} \sin 2\theta \right)^2 = \frac{k^2}{4} \sin^2 2\theta$
Multiply by 4:
$4q^2 = k^2 \sin^2 2\theta$
... (ii)
Proving the relation:
Add equations (i) and (ii):
$p^2 + 4q^2 = k^2 \cos^2 2\theta + k^2 \sin^2 2\theta$
$p^2 + 4q^2 = k^2 (\cos^2 2\theta + \sin^2 2\theta)$
Using the identity $\cos^2 \alpha + \sin^2 \alpha = 1$, where $\alpha = 2\theta$:
$p^2 + 4q^2 = k^2 (1)$
$p^2 + 4q^2 = k^2$
Hence, proved.
Question 17. In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
Answer:
Given:
The vertices of triangle ABC are A(2, 3), B(4, –1), and C(1, 2).
To Find:
1. The equation of the altitude from vertex A.
2. The length of the altitude from vertex A.
Solution:
Let AD be the altitude from vertex A to the side BC. By definition, the altitude AD is perpendicular to the side BC.
1. Finding the equation of the altitude from A:
First, find the slope of the side BC using the coordinates B(4, –1) and C(1, 2).
Slope of BC ($m_{BC}$) = $\frac{y₂ - y₁}{x₂ - x₁} = \frac{2 - (-1)}{1 - 4} = \frac{2 + 1}{-3} = \frac{3}{-3} = -1$.
Since the altitude AD is perpendicular to BC, the product of their slopes is -1.
Let the slope of the altitude AD be $m_{AD}$.
$m_{AD} \times m_{BC} = -1$
$m_{AD} \times (-1) = -1$
$m_{AD} = \frac{-1}{-1} = 1$.
Now, we find the equation of the line AD, which passes through vertex A(2, 3) and has a slope $m_{AD} = 1$.
Using the point-slope form $y - y₁ = m(x - x₁)$:
$y - 3 = 1(x - 2)$
$y - 3 = x - 2$
Rearranging into the standard form $Ax + By + C = 0$:
$x - y - 2 + 3 = 0$
$x - y + 1 = 0$
This is the equation of the altitude from vertex A.
2. Finding the length of the altitude from A:
The length of the altitude AD is the perpendicular distance from the point A(2, 3) to the line containing the side BC.
First, find the equation of the line BC. We know its slope $m_{BC} = -1$ and it passes through B(4, –1) (or C(1, 2)). Using point B:
$y - (-1) = -1(x - 4)$
$y + 1 = -x + 4$
$x + y + 1 - 4 = 0$
$x + y - 3 = 0$.
Now, calculate the perpendicular distance from point A(2, 3) to the line $x + y - 3 = 0$.
The formula for the distance 'd' of a point $(x₁, y₁)$ from the line $Ax + By + C = 0$ is:
$d = \frac{|Ax₁ + By₁ + C|}{\sqrt{A² + B²}}$
Here, $(x₁, y₁) = (2, 3)$ and the line is $x + y - 3 = 0$, so $A = 1$, $B = 1$, $C = -3$.
Length of altitude AD = $\frac{|1(2) + 1(3) - 3|}{\sqrt{(1)² + (1)²}}$
Length of altitude AD = $\frac{|2 + 3 - 3|}{\sqrt{1 + 1}}$
Length of altitude AD = $\frac{|2|}{\sqrt{2}}$
Length of altitude AD = $\frac{2}{\sqrt{2}} = \frac{2\sqrt{2}}{2} = \sqrt{2}$.
Therefore, the length of the altitude from vertex A is $\sqrt{2}$ units.
Summary:
The equation of the altitude from vertex A is $x - y + 1 = 0$.
The length of the altitude from vertex A is $\sqrt{2}$ units.
Question 18. If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that $\frac{1}{p^{2}}$ = $\frac{1}{a^{2}}$ + $\frac{1}{b^{2}}$
Answer:
Given:
A line has intercepts $a$ (on the x-axis) and $b$ (on the y-axis).
$p$ is the length of the perpendicular from the origin (0, 0) to this line.
To Prove:
$\frac{1}{p^{2}} = \frac{1}{a^{2}} + \frac{1}{b^{2}}$
Proof:
The equation of a line in intercept form is given by:
$\frac{x}{a} + \frac{y}{b} = 1$
To find the perpendicular distance from the origin, we first convert this equation to the standard form $Ax + By + C = 0$.
Multiply the equation by $ab$ (assuming $a \neq 0, b \neq 0$):
$ab \left( \frac{x}{a} \right) + ab \left( \frac{y}{b} \right) = ab(1)$
$bx + ay = ab$
$bx + ay - ab = 0$
Comparing this with the standard form $Ax + By + C = 0$, we have:
$A = b$, $B = a$, $C = -ab$.
The formula for the perpendicular distance $p$ from a point $(x₁, y₁)$ to the line $Ax + By + C = 0$ is:
$p = \frac{|Ax₁ + By₁ + C|}{\sqrt{A² + B²}}$
In this case, the point $(x₁, y₁) = (0, 0)$ (the origin).
Substituting the values of A, B, C, $x₁$, and $y₁$:
$p = \frac{|b(0) + a(0) - ab|}{\sqrt{b² + a²}}$
$p = \frac{|-ab|}{\sqrt{a² + b²}}$
$p = \frac{|ab|}{\sqrt{a² + b²}}$
Since $p$ is a length, $p > 0$. Squaring both sides:
$p² = \left( \frac{|ab|}{\sqrt{a² + b²}} \right)²$
$p² = \frac{(|ab|)²}{(\sqrt{a² + b²})²}$
$p² = \frac{a²b²}{a² + b²}$
Now, take the reciprocal of both sides:
$\frac{1}{p²} = \frac{a² + b²}{a²b²}$
Split the fraction on the right-hand side:
$\frac{1}{p²} = \frac{a²}{a²b²} + \frac{b²}{a²b²}$
Cancel the common terms in each fraction:
$\frac{1}{p²} = \frac{\cancel{a²}}{\cancel{a²}b²} + \frac{\cancel{b²}}{a²\cancel{b²}}$
$\frac{1}{p²} = \frac{1}{b²} + \frac{1}{a²}$
Rearranging the terms:
$\frac{1}{p²} = \frac{1}{a²} + \frac{1}{b²}$
Hence, proved.
Example 20 to 25 - Miscellaneous Examples
Example 20: If the lines 2x + y - 3 = 5, 5x + ky - 3 = 0 and 3x - y = 2 are concurrent, find the value of k.
Answer:
Given:
The equations of the three lines are:
Line 1: $2x + y - 3 = 5$
Simplifying Line 1:
$2x + y - 3 - 5 = 0$
$2x + y - 8 = 0$
... (i)
Line 2:
$5x + ky - 3 = 0$
... (ii)
Line 3: $3x - y = 2$
Simplifying Line 3:
$3x - y - 2 = 0$
... (iii)
The three lines are concurrent, which means they intersect at a single common point.
To Find:
The value of $k$.
Solution:
Method 1: Solving two equations and substituting into the third
Since the lines are concurrent, the point of intersection of any two lines must lie on the third line. We will find the point of intersection of lines (i) and (iii) (as they do not involve $k$).
Consider equations (i) and (iii):
$2x + y - 8 = 0$
... (i)
$3x - y - 2 = 0$
... (iii)
Adding equation (i) and equation (iii) to eliminate $y$:
$(2x + y - 8) + (3x - y - 2) = 0 + 0$
$2x + 3x + y - y - 8 - 2 = 0$
$5x - 10 = 0$
$5x = 10$
$x = \frac{10}{5}$
$\mathbf{x = 2}$
Now, substitute the value of $x = 2$ into equation (i) to find $y$:
$2(2) + y - 8 = 0$
$4 + y - 8 = 0$
$y - 4 = 0$
$\mathbf{y = 4}$
So, the point of intersection of lines (i) and (iii) is $(2, 4)$.
Since the lines are concurrent, this point $(2, 4)$ must also satisfy equation (ii):
$5x + ky - 3 = 0$
... (ii)
Substitute $x = 2$ and $y = 4$ into equation (ii):
$5(2) + k(4) - 3 = 0$
$10 + 4k - 3 = 0$
$7 + 4k = 0$
$4k = -7$
$k = -\frac{7}{4}$
Method 2: Using Determinant Condition for Concurrency
Three lines $a_1x + b_1y + c_1 = 0$, $a_2x + b_2y + c_2 = 0$, and $a_3x + b_3y + c_3 = 0$ are concurrent if the determinant of the coefficients is zero:
$\begin{vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end{vmatrix} = 0$
The given lines in the required format are:
$2x + 1y - 8 = 0$
$5x + ky - 3 = 0$
$3x - 1y - 2 = 0$
So, we must have:
$\begin{vmatrix} 2 & 1 & -8 \\ 5 & k & -3 \\ 3 & -1 & -2 \end{vmatrix} = 0$
Expanding the determinant along the first row:
$2 \begin{vmatrix} k & -3 \\ -1 & -2 \end{vmatrix} - 1 \begin{vmatrix} 5 & -3 \\ 3 & -2 \end{vmatrix} + (-8) \begin{vmatrix} 5 & k \\ 3 & -1 \end{vmatrix} = 0$
$2(k(-2) - (-3)(-1)) - 1(5(-2) - (-3)(3)) - 8(5(-1) - k(3)) = 0$
$2(-2k - 3) - 1(-10 - (-9)) - 8(-5 - 3k) = 0$
$2(-2k - 3) - 1(-10 + 9) - 8(-5 - 3k) = 0$
$2(-2k - 3) - 1(-1) - 8(-5 - 3k) = 0$
$-4k - 6 + 1 + 40 + 24k = 0$
(-4k + 24k) + (-6 + 1 + 40) = 0$
$20k + 35 = 0$
$20k = -35$
$k = -\frac{35}{20}$
$k = -\frac{7 \times 5}{4 \times 5}$
$k = -\frac{7}{4}$
Final Answer:
Both methods yield the same result. The value of $k$ for which the lines are concurrent is $\mathbf{-\frac{7}{4}}$.
Example 21: Find the distance of the line 4x – y = 0 from the point P (4, 1) measured along the line making an angle of 135° with the positive x-axis.
Answer:
Given:
Equation of the line: $4x - y = 0$.
Point: $P(4, 1)$.
The distance is measured along a line passing through $P(4, 1)$ and making an angle of $135^\circ$ with the positive x-axis.
To Find:
The distance of the line $4x - y = 0$ from the point $P(4, 1)$ measured along the given direction.
Solution:
Let the given line be $L_1$. Its equation is $4x - y = 0$.
Let the line along which the distance is measured be $L_2$. This line passes through the point $P(4, 1)$ and makes an angle of $135^\circ$ with the positive x-axis.
The slope of line $L_2$ is given by $m = \tan\theta$, where $\theta = 135^\circ$.
Slope of $L_2$, $m = \tan(135^\circ)$
... (i)
Since $\tan(135^\circ) = \tan(180^\circ - 45^\circ) = -\tan(45^\circ) = -1$, the slope of $L_2$ is $-1$.
$m = -1$
... (ii)
The equation of line $L_2$ passing through $P(4, 1)$ with slope $m = -1$ can be found using the point-slope form $y - y_1 = m(x - x_1)$.
$y - 1 = -1(x - 4)$
Substitute $P(4,1)$ and $m=-1$
$y - 1 = -x + 4$
$x + y - 5 = 0$
Equation of line $L_2$ ... (iii)
The distance required is the distance between point $P(4, 1)$ and the intersection point of line $L_1$ ($4x - y = 0$) and line $L_2$ ($x + y - 5 = 0$).
Let $Q(x, y)$ be the intersection point of $L_1$ and $L_2$. We need to solve the system of equations:
$4x - y = 0$
... (iv)
$x + y - 5 = 0$
... (v)
From equation (iv), we get $y = 4x$.
Substitute $y = 4x$ into equation (v):
$x + (4x) - 5 = 0$
Substitute $y=4x$ into (v)
$5x - 5 = 0$
$5x = 5$
$x = 1$
x-coordinate of Q
Now, substitute $x = 1$ back into $y = 4x$ to find the y-coordinate:
$y = 4(1)$
Substitute $x=1$ into $y=4x$
$y = 4$
y-coordinate of Q
So, the intersection point $Q$ is $(1, 4)$.
The distance of the line $4x - y = 0$ from point $P(4, 1)$ measured along line $L_2$ is the distance between points $P(4, 1)$ and $Q(1, 4)$.
Using the distance formula between two points $(x_1, y_1)$ and $(x_2, y_2)$, which is $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$:
Distance $PQ = \sqrt{(1 - 4)^2 + (4 - 1)^2}$
Using distance formula
Distance $PQ = \sqrt{(-3)^2 + (3)^2}$
Distance $PQ = \sqrt{9 + 9}$
Distance $PQ = \sqrt{18}$
Distance $PQ = \sqrt{9 \times 2}$
Distance $PQ = 3\sqrt{2}$
Thus, the distance of the line $4x - y = 0$ from the point $P(4, 1)$ measured along the line making an angle of $135^\circ$ with the positive x-axis is $3\sqrt{2}$ units.
Example 22: Assuming that straight lines work as the plane mirror for a point, find the image of the point (1, 2) in the line x – 3y + 4 = 0.
Answer:
Given:
Point $P$ with coordinates $(1, 2)$.
Line $L$ (acting as a plane mirror) with equation $x - 3y + 4 = 0$.
To Find:
The image of the point $P(1, 2)$ in the line $x - 3y + 4 = 0$.
Solution:
Let the image of the point $P(1, 2)$ in the line $x - 3y + 4 = 0$ be the point $Q(x', y')$.
For $Q$ to be the image of $P$ in the line $L$, two geometric conditions must hold:
1. The line segment $PQ$ is perpendicular to the mirror line $L$.
2. The midpoint of the line segment $PQ$ lies on the mirror line $L$.
First, let's find the slope of the mirror line $L$. The equation is $x - 3y + 4 = 0$.
$-3y = -x - 4$
$3y = x + 4$
$y = \frac{1}{3}x + \frac{4}{3}$
The slope of the mirror line $L$ is $m_L = \frac{1}{3}$.
The slope of the line segment $PQ$ joining $P(1, 2)$ and $Q(x', y')$ is $m_{PQ} = \frac{y' - 2}{x' - 1}$.
Since $PQ$ is perpendicular to $L$, the product of their slopes is $-1$.
$m_{PQ} \times m_L = -1$
Perpendicularity condition
$\left(\frac{y' - 2}{x' - 1}\right) \times \left(\frac{1}{3}\right) = -1$
$\frac{y' - 2}{x' - 1} = -3$
$y' - 2 = -3(x' - 1)$
$y' - 2 = -3x' + 3$
$3x' + y' = 5$
... (i)
Next, consider the midpoint of the line segment $PQ$. Let $M$ be the midpoint of $PQ$.
The coordinates of the midpoint $M$ are given by $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Coordinates of $M = \left(\frac{1 + x'}{2}, \frac{2 + y'}{2}\right)$
Using midpoint formula
The midpoint $M$ must lie on the mirror line $x - 3y + 4 = 0$. Substitute the coordinates of $M$ into the equation of the line.
$\left(\frac{1 + x'}{2}\right) - 3\left(\frac{2 + y'}{2}\right) + 4 = 0$
Midpoint M satisfies line equation
Multiply the entire equation by 2 to clear the denominators:
$2 \times \left[ \left(\frac{1 + x'}{2}\right) - 3\left(\frac{2 + y'}{2}\right) + 4 \right] = 2 \times 0$
$(1 + x') - 3(2 + y') + 8 = 0$
$1 + x' - 6 - 3y' + 8 = 0$
$x' - 3y' + 3 = 0$
... (ii)
Now we need to solve the system of two linear equations for $x'$ and $y'$:
$(i) \quad 3x' + y' = 5$
$(ii) \quad x' - 3y' = -3$
From equation (i), we can express $y'$ in terms of $x'$:
$y' = 5 - 3x'$
From (i)
Substitute this expression for $y'$ into equation (ii):
$x' - 3(5 - 3x') = -3$
Substitute $y'$ into (ii)
$x' - 15 + 9x' = -3$
$10x' - 15 = -3$
$10x' = -3 + 15$
$10x' = 12$
$x' = \frac{12}{10} = \frac{6}{5}$
Now substitute the value of $x' = \frac{6}{5}$ back into the expression for $y'$ ($y' = 5 - 3x'$):
$y' = 5 - 3\left(\frac{6}{5}\right)$
Substitute $x'$ value
$y' = 5 - \frac{18}{5}$
$y' = \frac{25}{5} - \frac{18}{5}$
$y' = \frac{7}{5}$
Therefore, the coordinates of the image point $Q(x', y')$ are $\left(\frac{6}{5}, \frac{7}{5}\right)$.
Alternate Solution (Using Formula):
The image $(x', y')$ of a point $(x_1, y_1)$ in the line $ax + by + c = 0$ is given by the formula:
$\frac{x' - x_1}{a} = \frac{y' - y_1}{b} = \frac{-2(ax_1 + by_1 + c)}{a^2 + b^2}$
Image formula
Given point $(x_1, y_1) = (1, 2)$ and the line $x - 3y + 4 = 0$, we have $a=1$, $b=-3$, and $c=4$.
Substitute these values into the formula:
$\frac{x' - 1}{1} = \frac{y' - 2}{-3} = \frac{-2(1(1) + (-3)(2) + 4)}{1^2 + (-3)^2}$
$\frac{x' - 1}{1} = \frac{y' - 2}{-3} = \frac{-2(1 - 6 + 4)}{1 + 9}$
$\frac{x' - 1}{1} = \frac{y' - 2}{-3} = \frac{-2(-1)}{10}$
$\frac{x' - 1}{1} = \frac{y' - 2}{-3} = \frac{2}{10}$
$\frac{x' - 1}{1} = \frac{y' - 2}{-3} = \frac{1}{5}$
Simplified expression
Equating the first part to $\frac{1}{5}$:
$\frac{x' - 1}{1} = \frac{1}{5}$
$x' - 1 = \frac{1}{5}$
$x' = 1 + \frac{1}{5} = \frac{5+1}{5} = \frac{6}{5}$
Equating the second part to $\frac{1}{5}$:
$\frac{y' - 2}{-3} = \frac{1}{5}$
$y' - 2 = -3 \times \frac{1}{5} = -\frac{3}{5}$
$y' = 2 - \frac{3}{5} = \frac{10 - 3}{5} = \frac{7}{5}$
Using the formula, the image point is $\left(\frac{6}{5}, \frac{7}{5}\right)$, which matches the result obtained using the geometric method.
The image of the point $(1, 2)$ in the line $x - 3y + 4 = 0$ is $\left(\frac{6}{5}, \frac{7}{5}\right)$.
Example 23: Show that the area of the triangle formed by the lines y = m1x + c1 , y = m2x + c2 and x = 0 is $\frac{\left( c_1 \;-\; c_2 \right)^2}{2\left| m_1 \;-\; m_2 \right|}$ .
Answer:
Given:
The equations of three lines:
$L_1: y = m_1x + c_1$
$L_2: y = m_2x + c_2$
$L_3: x = 0$ (This is the y-axis)
To Show:
The area of the triangle formed by these three lines is $\frac{\left( c_1 \;-\; c_2 \right)^2}{2\left| m_1 \;-\; m_2 \right|}$.
Solution:
To find the area of the triangle, we need to determine the coordinates of its vertices. The vertices are the points of intersection of the given lines taken pairwise.
Vertex 1: Intersection of $L_1$ ($y = m_1x + c_1$) and $L_3$ ($x = 0$)
Substitute $x = 0$ into the equation of $L_1$:
$y = m_1(0) + c_1$
Substitute $x=0$ into $L_1$
$y = c_1$
The first vertex is $A(0, c_1)$. This point lies on the y-axis ($x=0$).
Vertex 2: Intersection of $L_2$ ($y = m_2x + c_2$) and $L_3$ ($x = 0$)
Substitute $x = 0$ into the equation of $L_2$:
$y = m_2(0) + c_2$
Substitute $x=0$ into $L_2$
$y = c_2$
The second vertex is $B(0, c_2)$. This point also lies on the y-axis ($x=0$).
Vertex 3: Intersection of $L_1$ ($y = m_1x + c_1$) and $L_2$ ($y = m_2x + c_2$)
To find the intersection point, we set the y-values equal:
$m_1x + c_1 = m_2x + c_2$
Rearranging the terms to solve for $x$:
$(m_1 - m_2)x = c_2 - c_1$
Assuming $m_1 \neq m_2$ (for the lines to intersect and form a triangle), we get:
$x = \frac{c_2 - c_1}{m_1 - m_2}$
Now substitute this value of $x$ back into the equation of $L_1$ (or $L_2$) to find the corresponding $y$ value:
$y = m_1\left(\frac{c_2 - c_1}{m_1 - m_2}\right) + c_1$
Substitute x-coordinate into $L_1$
$y = \frac{m_1(c_2 - c_1) + c_1(m_1 - m_2)}{m_1 - m_2}$
$y = \frac{m_1c_2 - m_1c_1 + m_1c_1 - c_1m_2}{m_1 - m_2}$
$y = \frac{m_1c_2 - c_1m_2}{m_1 - m_2}$
The third vertex is $C\left(\frac{c_2 - c_1}{m_1 - m_2}, \frac{m_1c_2 - c_1m_2}{m_1 - m_2}\right)$.
The three vertices of the triangle are $A(0, c_1)$, $B(0, c_2)$, and $C\left(\frac{c_2 - c_1}{m_1 - m_2}, \frac{m_1c_2 - c_1m_2}{m_1 - m_2}\right)$.
We can calculate the area of the triangle using the base and height.
The base of the triangle can be taken as the line segment AB, which lies on the y-axis ($x=0$). The length of the base is the distance between the points A and B.
Base length = $\sqrt{(0 - 0)^2 + (c_2 - c_1)^2}$
Distance formula
Base length = $\sqrt{(c_2 - c_1)^2}$
Base length = $|c_2 - c_1|$
Length of base AB ... (i)
The height of the triangle is the perpendicular distance from the vertex C to the base AB (the line $x=0$). The perpendicular distance of a point $(x_0, y_0)$ from the y-axis ($x=0$) is $|x_0|$.
Height = $\left|\frac{c_2 - c_1}{m_1 - m_2}\right|$
Absolute value of x-coordinate of C
Height = $\frac{|c_2 - c_1|}{|m_1 - m_2|}$
Height of the triangle ... (ii)
The area of a triangle is given by the formula: Area = $\frac{1}{2} \times \text{base} \times \text{height}$.
Using the base length from (i) and the height from (ii):
Area = $\frac{1}{2} \times |c_2 - c_1| \times \frac{|c_2 - c_1|}{|m_1 - m_2|}$
Area = $\frac{1}{2} \times \frac{|c_2 - c_1|^2}{|m_1 - m_2|}$
Since $|a|^2 = a^2$ for any real number $a$, we have $|c_2 - c_1|^2 = (c_2 - c_1)^2$.
Area = $\frac{(c_2 - c_1)^2}{2|m_1 - m_2|}$
We know that $(c_2 - c_1)^2 = (c_1 - c_2)^2$ and $|m_1 - m_2| = |m_2 - m_1|$. Therefore, we can write the area as:
Area = $\frac{\left( c_1 \;-\; c_2 \right)^2}{2\left| m_1 \;-\; m_2 \right|}$
This matches the required expression for the area of the triangle.
Example 24: A line is such that its segment between the lines 5x – y + 4 = 0 and 3x + 4y – 4 = 0 is bisected at the point (1, 5). Obtain its equation.
Answer:
Given:
Two lines with equations:
$L_1: 5x - y + 4 = 0$
$L_2: 3x + 4y - 4 = 0$
A point $P(1, 5)$ which is the midpoint of the segment of a required line intercepted between $L_1$ and $L_2$.
To Find:
The equation of the line whose segment between $L_1$ and $L_2$ is bisected at $P(1, 5)$.
Solution:
Let the required line be $L$. Let this line $L$ intersect line $L_1$ at point $A(x_1, y_1)$ and line $L_2$ at point $B(x_2, y_2)$.
The point $P(1, 5)$ is the midpoint of the line segment $AB$. Using the midpoint formula, we have:
$\frac{x_1 + x_2}{2} = 1$
x-coordinate of midpoint
y-coordinate of midpoint
From these equations, we get:
$x_1 + x_2 = 2$
... (i)
$y_1 + y_2 = 10$
... (ii)
Since the point $A(x_1, y_1)$ lies on line $L_1$ ($5x - y + 4 = 0$), it must satisfy the equation of $L_1$:
$5x_1 - y_1 + 4 = 0$
A lies on $L_1$ ... (iii)
Since the point $B(x_2, y_2)$ lies on line $L_2$ ($3x + 4y - 4 = 0$), it must satisfy the equation of $L_2$:
$3x_2 + 4y_2 - 4 = 0$
B lies on $L_2$ ... (iv)
We now have a system of four linear equations with four variables ($x_1, y_1, x_2, y_2$). We can solve this system to find the coordinates of A and B.
From (i), $x_2 = 2 - x_1$.
From (ii), $y_2 = 10 - y_1$.
From (iii), $y_1 = 5x_1 + 4$.
Substitute the expression for $y_1$ into the expression for $y_2$:
$y_2 = 10 - (5x_1 + 4)$
Substitute $y_1$ into $y_2$ expression
$y_2 = 10 - 5x_1 - 4$
$y_2 = 6 - 5x_1$
Now substitute the expressions for $x_2$ and $y_2$ into equation (iv):
$3(2 - x_1) + 4(6 - 5x_1) - 4 = 0$
Substitute $x_2, y_2$ into (iv)
$6 - 3x_1 + 24 - 20x_1 - 4 = 0$
$30 - 23x_1 - 4 = 0$
$26 - 23x_1 = 0$
$23x_1 = 26$
$x_1 = \frac{26}{23}$
x-coordinate of A
Now find $y_1$ using the relation $y_1 = 5x_1 + 4$:
$y_1 = 5\left(\frac{26}{23}\right) + 4$
Substitute $x_1$ value
$y_1 = \frac{130}{23} + \frac{4 \times 23}{23}$
$y_1 = \frac{130 + 92}{23}$
$y_1 = \frac{222}{23}$
y-coordinate of A
So, the coordinates of point $A$ are $\left(\frac{26}{23}, \frac{222}{23}\right)$.
The required line passes through the point $P(1, 5)$ and the point $A\left(\frac{26}{23}, \frac{222}{23}\right)$.
We can find the equation of the line passing through these two points using the two-point form $\frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1}$. Using $P(1, 5)$ as $(x_1, y_1)$ and $A\left(\frac{26}{23}, \frac{222}{23}\right)$ as $(x_2, y_2)$.
First, calculate the slope $m = \frac{y_2 - y_1}{x_2 - x_1}$:
$m = \frac{\frac{222}{23} - 5}{\frac{26}{23} - 1}$
$m = \frac{\frac{222 - 5 \times 23}{23}}{\frac{26 - 1 \times 23}{23}}$
$m = \frac{\frac{222 - 115}{23}}{\frac{26 - 23}{23}}$
$m = \frac{\frac{107}{23}}{\frac{3}{23}}$
$m = \frac{107}{3}$
Slope of the required line
Now, use the point-slope form $y - y_1 = m(x - x_1)$ with point $P(1, 5)$ and slope $m = \frac{107}{3}$:
$y - 5 = \frac{107}{3}(x - 1)$
Point-slope form
Multiply both sides by 3:
$3(y - 5) = 107(x - 1)$
$3y - 15 = 107x - 107$
Rearrange the terms to the general form $Ax + By + C = 0$:
$107x - 3y - 107 + 15 = 0$
$107x - 3y - 92 = 0$
Equation of the required line
The equation of the line is $107x - 3y - 92 = 0$.
Example 25: Show that the path of a moving point such that its distances from two lines 3x – 2y = 5 and 3x + 2y = 5 are equal is a straight line.
Answer:
Given:
Two lines with equations:
$L_1: 3x - 2y = 5 \implies 3x - 2y - 5 = 0$
$L_2: 3x + 2y = 5 \implies 3x + 2y - 5 = 0$
To Show:
The locus (path) of a moving point whose distance from $L_1$ is equal to its distance from $L_2$ is a straight line.
Solution:
Let $P(x, y)$ be the coordinates of the moving point.
The distance of a point $(x_0, y_0)$ from a line $Ax + By + C = 0$ is given by the formula $\frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$.
The distance of the point $P(x, y)$ from line $L_1$ ($3x - 2y - 5 = 0$) is:
$d_1 = \frac{|3x - 2y - 5|}{\sqrt{3^2 + (-2)^2}}$
$d_1 = \frac{|3x - 2y - 5|}{\sqrt{9 + 4}}$
$d_1 = \frac{|3x - 2y - 5|}{\sqrt{13}}$
Distance from $L_1$ ... (i)
The distance of the point $P(x, y)$ from line $L_2$ ($3x + 2y - 5 = 0$) is:
$d_2 = \frac{|3x + 2y - 5|}{\sqrt{3^2 + 2^2}}$
$d_2 = \frac{|3x + 2y - 5|}{\sqrt{9 + 4}}$
$d_2 = \frac{|3x + 2y - 5|}{\sqrt{13}}$
Distance from $L_2$ ... (ii)
According to the problem statement, the distance of the moving point from the two lines is equal, i.e., $d_1 = d_2$.
$\frac{|3x - 2y - 5|}{\sqrt{13}} = \frac{|3x + 2y - 5|}{\sqrt{13}}$
Given condition $d_1=d_2$
Multiply both sides by $\sqrt{13}$:
$|3x - 2y - 5| = |3x + 2y - 5|$
This equation implies that the expression inside the absolute value on the left is either equal to or the negative of the expression inside the absolute value on the right.
Case 1: $3x - 2y - 5 = 3x + 2y - 5$
Subtract $3x$ from both sides:
$-2y - 5 = 2y - 5$
Add $5$ to both sides:
$-2y = 2y$
Add $2y$ to both sides:
$0 = 4y$
$y = 0$
Equation from Case 1
Case 2: $3x - 2y - 5 = -(3x + 2y - 5)$
$3x - 2y - 5 = -3x - 2y + 5$
Add $3x$ to both sides:
$6x - 2y - 5 = -2y + 5$
Add $2y$ to both sides:
$6x - 5 = 5$
Add $5$ to both sides:
$6x = 10$
Divide both sides by 6:
$x = \frac{10}{6}$
$x = \frac{5}{3}$
Equation from Case 2
The locus of the moving point $P(x, y)$ is given by the equations obtained from Case 1 and Case 2: $y = 0$ and $x = \frac{5}{3}$.
The equation $y = 0$ represents the x-axis, which is a straight line.
The equation $x = \frac{5}{3}$ represents a vertical line parallel to the y-axis, which is also a straight line.
Thus, the path of the moving point is a straight line (or consists of two straight lines). These lines are the angle bisectors of the angles formed by the given lines $L_1$ and $L_2$.
Since the equations obtained are linear equations in $x$ and $y$, they represent straight lines. Therefore, the path of the moving point is a straight line.
Miscellaneous Exercise on Chapter 10
Question 1. Find the values of k for which the line (k – 3) x – (4 – k2) y + k2 – 7k + 6 = 0 is
(a) Parallel to the x-axis,
(b) Parallel to the y-axis,
(c) Passing through the origin.
Answer:
Given:
The equation of a line: $(k – 3) x – (4 – k^2) y + k^2 – 7k + 6 = 0$.
This equation is in the general form $Ax + By + C = 0$, where:
$A = k - 3$
$B = -(4 - k^2) = k^2 - 4$
$C = k^2 - 7k + 6$
To Find:
The values of $k$ for which the line is:
(a) Parallel to the x-axis.
(b) Parallel to the y-axis.
(c) Passing through the origin.
Solution:
The general equation of a straight line is $Ax + By + C = 0$.
(a) Parallel to the x-axis:
A line is parallel to the x-axis if and only if the coefficient of $x$ is zero ($A = 0$) and the coefficient of $y$ is non-zero ($B \neq 0$).
From the given equation, the coefficient of $x$ is $A = k - 3$.
Set $A = 0$:
$k - 3 = 0$
$k = 3$
Now, check if the coefficient of $y$, $B = k^2 - 4$, is non-zero when $k = 3$.
$B = (3)^2 - 4$
Substitute $k=3$ into $B$
$B = 9 - 4$
$B = 5$
Since $B = 5 \neq 0$, the condition is satisfied.
Therefore, the line is parallel to the x-axis when $k = 3$.
(b) Parallel to the y-axis:
A line is parallel to the y-axis if and only if the coefficient of $y$ is zero ($B = 0$) and the coefficient of $x$ is non-zero ($A \neq 0$).
From the given equation, the coefficient of $y$ is $B = k^2 - 4$.
Set $B = 0$:
$k^2 - 4 = 0$
$(k - 2)(k + 2) = 0$
This gives two possible values for $k$: $k = 2$ or $k = -2$.
Now, check if the coefficient of $x$, $A = k - 3$, is non-zero for these values of $k$.
If $k = 2$:
$A = 2 - 3 = -1$
Since $A = -1 \neq 0$, the condition is satisfied for $k = 2$.
If $k = -2$:
$A = -2 - 3 = -5$
Since $A = -5 \neq 0$, the condition is satisfied for $k = -2$.
Therefore, the line is parallel to the y-axis when $k = 2$ or $k = -2$.
(c) Passing through the origin:
A line $Ax + By + C = 0$ passes through the origin $(0, 0)$ if substituting $x = 0$ and $y = 0$ into the equation results in a true statement. This happens if and only if the constant term $C$ is zero.
From the given equation, the constant term is $C = k^2 - 7k + 6$.
Set $C = 0$:
$k^2 - 7k + 6 = 0$
Factor the quadratic equation:
$(k - 1)(k - 6) = 0$
This gives two possible values for $k$: $k = 1$ or $k = 6$.
Therefore, the line passes through the origin when $k = 1$ or $k = 6$.
Summary of results:
(a) The line is parallel to the x-axis when $k = 3$.
(b) The line is parallel to the y-axis when $k = 2$ or $k = -2$.
(c) The line passes through the origin when $k = 1$ or $k = 6$.
Question 2. Find the values of θ and p, if the equation x cos θ + y sin θ = p is the normal form of the line $\sqrt{3}$x + y + 2 = 0.
Answer:
Given:
The equation of a line is $\sqrt{3}x + y + 2 = 0$.
The normal form of the line is $x \cos \theta + y \sin \theta = p$.
To Find:
The values of $\theta$ and $p$.
Solution:
The equation of the given line is $\sqrt{3}x + y + 2 = 0$.
We need to convert this equation into the normal form $x \cos \theta + y \sin \theta = p$, where $p \ge 0$.
The general form of the line is $Ax + By + C = 0$. Here, $A = \sqrt{3}$, $B = 1$, and $C = 2$.
To convert the general form to the normal form, we divide the equation by $\pm\sqrt{A^2 + B^2}$. The sign is chosen such that the constant term on the right side becomes positive ($p$).
Calculate $\sqrt{A^2 + B^2}$:
$\sqrt{A^2 + B^2} = \sqrt{(\sqrt{3})^2 + (1)^2}$
$\sqrt{A^2 + B^2} = \sqrt{3 + 1}$
$\sqrt{A^2 + B^2} = \sqrt{4}$
$\sqrt{A^2 + B^2} = 2$
The given equation is $\sqrt{3}x + y + 2 = 0$. Rewrite it with the constant term on the right side:
$\sqrt{3}x + y = -2$
Since $p$ must be non-negative, we need to make the right side positive. Multiply the entire equation by $-1$:
$-\sqrt{3}x - y = 2$
Equation ready for normal form division
Now, divide the equation $-\sqrt{3}x - y = 2$ by $2$ (the value of $\sqrt{A^2 + B^2}$):
$\frac{-\sqrt{3}}{2}x - \frac{1}{2}y = \frac{2}{2}$
$-\frac{\sqrt{3}}{2}x - \frac{1}{2}y = 1$
Equation in normal form
Compare this equation with the normal form $x \cos \theta + y \sin \theta = p$:
$\cos \theta = -\frac{\sqrt{3}}{2}$
... (i)
$\sin \theta = -\frac{1}{2}$
... (ii)
$p = 1$
... (iii)
From equations (i) and (ii), we need to find the angle $\theta$ such that its cosine is $-\frac{\sqrt{3}}{2}$ and its sine is $-\frac{1}{2}$.
Since both $\cos \theta$ and $\sin \theta$ are negative, the angle $\theta$ must lie in the third quadrant.
The angle whose cosine is $\frac{\sqrt{3}}{2}$ and sine is $\frac{1}{2}$ is $30^\circ$ or $\frac{\pi}{6}$ radians.
In the third quadrant, the angle $\theta$ can be found by adding $180^\circ$ (or $\pi$ radians) to the reference angle:
$\theta = 180^\circ + 30^\circ$
$\theta = 210^\circ$
Value of $\theta$ in degrees
In radians, the angle is:
$\theta = \pi + \frac{\pi}{6}$
$\theta = \frac{6\pi + \pi}{6}$
$\theta = \frac{7\pi}{6}$
Value of $\theta$ in radians
From equation (iii), the value of $p$ is $1$.
The values are $p = 1$ and $\theta = 210^\circ$ (or $\frac{7\pi}{6}$ radians).
Question 3. Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and – 6, respectively.
Answer:
Given:
Let the x-intercept of the line be $a$ and the y-intercept be $b$.
Sum of intercepts: $a + b = 1$
Product of intercepts: $ab = -6$
To Find:
The equations of the lines satisfying the given conditions.
Solution:
The equation of a line in the intercept form is given by $\frac{x}{a} + \frac{y}{b} = 1$, where $a$ is the x-intercept and $b$ is the y-intercept.
We are given the following system of equations:
$a + b = 1$
... (i)
$ab = -6$
... (ii)
From equation (i), we can express $b$ in terms of $a$:
$b = 1 - a$
From (i)
Substitute this expression for $b$ into equation (ii):
$a(1 - a) = -6$
Substitute $b$ into (ii)
$a - a^2 = -6$
Rearrange the terms to form a quadratic equation in $a$:
$a^2 - a - 6 = 0$
Quadratic equation for $a$
Factor the quadratic equation:
$(a - 3)(a + 2) = 0$
This gives two possible values for $a$:
$a = 3$ or $a = -2$
Now, find the corresponding values for $b$ using $b = 1 - a$.
Case 1: If $a = 3$
$b = 1 - 3$
Substitute $a=3$ into $b=1-a$
$b = -2$
The intercepts are $a = 3$ and $b = -2$. The equation of the line is:
$\frac{x}{3} + \frac{y}{-2} = 1$
To eliminate the denominators, multiply the equation by the LCM of 3 and -2, which is 6:
$6 \times \left(\frac{x}{3}\right) + 6 \times \left(\frac{y}{-2}\right) = 6 \times 1$
$2x - 3y = 6$
Rearranging to the general form:
$2x - 3y - 6 = 0$
Equation from Case 1
Case 2: If $a = -2$
$b = 1 - (-2)$
Substitute $a=-2$ into $b=1-a$
$b = 1 + 2$
$b = 3$
The intercepts are $a = -2$ and $b = 3$. The equation of the line is:
$\frac{x}{-2} + \frac{y}{3} = 1$
To eliminate the denominators, multiply the equation by the LCM of -2 and 3, which is 6:
$6 \times \left(\frac{x}{-2}\right) + 6 \times \left(\frac{y}{3}\right) = 6 \times 1$
$-3x + 2y = 6$
Rearranging to the general form:
$-3x + 2y - 6 = 0$
Equation from Case 2
This can also be written as $3x - 2y + 6 = 0$ by multiplying by $-1$.
There are two lines that satisfy the given conditions. Their equations are $2x - 3y - 6 = 0$ and $3x - 2y + 6 = 0$.
Question 4. What are the points on the y-axis whose distance from the line $\frac{x}{3}$ + $\frac{y}{4}$ = 1 is 4 units.
Answer:
Given:
The equation of the line: $\frac{x}{3} + \frac{y}{4} = 1$.
The distance from the line is 4 units.
The points are on the y-axis.
To Find:
The coordinates of the points on the y-axis whose distance from the given line is 4 units.
Solution:
Any point on the y-axis has coordinates $(0, y_0)$ for some value $y_0$.
The equation of the given line is $\frac{x}{3} + \frac{y}{4} = 1$.
To find the distance of a point from a line, we first convert the equation into the general form $Ax + By + C = 0$.
Multiply the equation by the least common multiple of 3 and 4, which is 12:
$12 \left(\frac{x}{3} + \frac{y}{4}\right) = 12 \times 1$
$4x + 3y = 12$
Rearrange into the general form:
$4x + 3y - 12 = 0$
General form of the line equation
The distance of a point $(x_0, y_0)$ from the line $Ax + By + C = 0$ is given by the formula:
$d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$
Distance formula
Here, the point is $(x_0, y_0) = (0, y_0)$, the line is $4x + 3y - 12 = 0$ ($A=4, B=3, C=-12$), and the distance $d = 4$.
Calculate $\sqrt{A^2 + B^2}$:
$\sqrt{A^2 + B^2} = \sqrt{4^2 + 3^2}$
$\sqrt{A^2 + B^2} = \sqrt{16 + 9}$
$\sqrt{A^2 + B^2} = \sqrt{25}$
$\sqrt{A^2 + B^2} = 5$
Substitute the values into the distance formula:
$4 = \frac{|4(0) + 3(y_0) - 12|}{5}$
$4 = \frac{|3y_0 - 12|}{5}$
Multiply both sides by 5:
$20 = |3y_0 - 12|$
This absolute value equation gives two possibilities:
Case 1: $3y_0 - 12 = 20$
$3y_0 = 20 + 12$
$3y_0 = 32$
$y_0 = \frac{32}{3}$
The point is $\left(0, \frac{32}{3}\right)$.
Case 2: $3y_0 - 12 = -20$
$3y_0 = -20 + 12$
$3y_0 = -8$
$y_0 = -\frac{8}{3}$
The point is $\left(0, -\frac{8}{3}\right)$.
Thus, there are two points on the y-axis whose distance from the given line is 4 units. The points are $\left(0, \frac{32}{3}\right)$ and $\left(0, -\frac{8}{3}\right)$.
Question 5. Find perpendicular distance from the origin to the line joining the points (cos θ, sin θ) and (cos φ, sin φ).
Answer:
Given:
Point 1: $A(\cos \theta, \sin \theta)$
Point 2: $B(\cos \phi, \sin \phi)$
Origin: $O(0, 0)$
To Find:
The perpendicular distance from the origin $O(0, 0)$ to the line joining the points $A(\cos \theta, \sin \theta)$ and $B(\cos \phi, \sin \phi)$.
Solution:
First, we find the equation of the line joining the points $A(x_1, y_1) = (\cos \theta, \sin \theta)$ and $B(x_2, y_2) = (\cos \phi, \sin \phi)$.
Using the two-point form of the equation of a line, which is $\frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1}$:
$\frac{y - \sin \theta}{x - \cos \theta} = \frac{\sin \phi - \sin \theta}{\cos \phi - \cos \theta}$
Two-point form
Rearrange the equation:
$(y - \sin \theta)(\cos \phi - \cos \theta) = (x - \cos \theta)(\sin \phi - \sin \theta)$
$y(\cos \phi - \cos \theta) - \sin \theta (\cos \phi - \cos \theta) = x(\sin \phi - \sin \theta) - \cos \theta (\sin \phi - \sin \theta)$
Rearrange to the general form $Ax + By + C = 0$:
$x(\sin \phi - \sin \theta) - y(\cos \phi - \cos \theta) + [\sin \theta (\cos \phi - \cos \theta) - \cos \theta (\sin \phi - \sin \theta)] = 0$
$x(\sin \phi - \sin \theta) + y(\cos \theta - \cos \phi) + [\sin \theta \cos \phi - \sin \theta \cos \theta - \cos \theta \sin \phi + \cos \theta \sin \theta] = 0$
$x(\sin \phi - \sin \theta) + y(\cos \theta - \cos \phi) + (\sin \theta \cos \phi - \cos \theta \sin \phi) = 0$
Using the trigonometric identity $\sin A \cos B - \cos A \sin B = \sin(A - B)$ for the constant term:
$x(\sin \phi - \sin \theta) + y(\cos \theta - \cos \phi) + \sin(\theta - \phi) = 0$
Equation of the line in general form ... (i)
This equation is in the form $Ax + By + C = 0$, where:
$A = \sin \phi - \sin \theta$
$B = \cos \theta - \cos \phi$
$C = \sin(\theta - \phi)$
The perpendicular distance from a point $(x_0, y_0)$ to the line $Ax + By + C = 0$ is given by $\frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$.
For the origin $(0, 0)$, the distance is $\frac{|A(0) + B(0) + C|}{\sqrt{A^2 + B^2}} = \frac{|C|}{\sqrt{A^2 + B^2}}$.
Calculate $\sqrt{A^2 + B^2}$:
$\sqrt{A^2 + B^2} = \sqrt{(\sin \phi - \sin \theta)^2 + (\cos \theta - \cos \phi)^2}$
$= \sqrt{\sin^2 \phi - 2\sin \phi \sin \theta + \sin^2 \theta + \cos^2 \theta - 2\cos \theta \cos \phi + \cos^2 \phi}$
$= \sqrt{(\sin^2 \phi + \cos^2 \phi) + (\sin^2 \theta + \cos^2 \theta) - 2(\cos \phi \cos \theta + \sin \phi \sin \theta)}$
Using the identity $\sin^2 x + \cos^2 x = 1$ and $\cos A \cos B + \sin A \sin B = \cos(A - B)$:
$= \sqrt{1 + 1 - 2 \cos(\phi - \theta)}$
$= \sqrt{2 - 2 \cos(\phi - \theta)}$
Using the identity $1 - \cos(2x) = 2\sin^2 x$, let $2x = \phi - \theta$, so $x = \frac{\phi - \theta}{2}$:
$= \sqrt{2 \times 2\sin^2\left(\frac{\phi - \theta}{2}\right)}$
$= \sqrt{4\sin^2\left(\frac{\phi - \theta}{2}\right)}$
$\sqrt{A^2 + B^2} = \left|2\sin\left(\frac{\phi - \theta}{2}\right)\right|$
Denominator for distance formula
The constant term is $C = \sin(\theta - \phi)$. Using the identity $\sin(-x) = -\sin x$, we have $C = -\sin(\phi - \theta)$.
Using the identity $\sin(2x) = 2\sin x \cos x$, let $2x = \phi - \theta$, so $x = \frac{\phi - \theta}{2}$:
$C = -2\sin\left(\frac{\phi - \theta}{2}\right) \cos\left(\frac{\phi - \theta}{2}\right)$
Numerator (absolute value) for distance formula
Now, substitute the values of $C$ and $\sqrt{A^2 + B^2}$ into the distance formula:
Distance $= \frac{|-2\sin\left(\frac{\phi - \theta}{2}\right) \cos\left(\frac{\phi - \theta}{2}\right)|}{\left|2\sin\left(\frac{\phi - \theta}{2}\right)\right|}$
Assuming the two points are distinct, $\phi - \theta \neq 2n\pi$, so $\sin\left(\frac{\phi - \theta}{2}\right) \neq 0$. We can cancel the common term:
Distance $= \frac{|-2| \left|\sin\left(\frac{\phi - \theta}{2}\right)\right| \left|\cos\left(\frac{\phi - \theta}{2}\right)\right|}{|2| \left|\sin\left(\frac{\phi - \theta}{2}\right)\right|}$
Distance $= \frac{2 \left|\cos\left(\frac{\phi - \theta}{2}\right)\right|}{2}$
Distance $= \left|\cos\left(\frac{\phi - \theta}{2}\right)\right|$
Alternatively, the equation of the line passing through $A(\cos \theta, \sin \theta)$ and $B(\cos \phi, \sin \phi)$ can be written in the form $x \cos \alpha + y \sin \alpha = p$.
The line passes through $A$ and $B$, which lie on the unit circle. A line passing through two points on a circle is a chord.
The angle of the normal to the line is the average of the angles $\theta$ and $\phi$ (or $\frac{\theta+\phi}{2}$).
The distance from the origin ($p$) is the projection of the position vector of one of the points onto the normal vector. Let's use point A $(\cos \theta, \sin \theta)$ and the normal direction $\alpha = \frac{\phi+\theta}{2}$.
$p = x_1 \cos \alpha + y_1 \sin \alpha$
Projection onto normal
$p = \cos \theta \cos\left(\frac{\phi+\theta}{2}\right) + \sin \theta \sin\left(\frac{\phi+\theta}{2}\right)$
Using the identity $\cos A \cos B + \sin A \sin B = \cos(A - B)$:
$p = \cos\left(\theta - \frac{\phi+\theta}{2}\right)$
$p = \cos\left(\frac{2\theta - \phi - \theta}{2}\right)$
$p = \cos\left(\frac{\theta - \phi}{2}\right)$
The equation of the line in normal form is $x \cos\left(\frac{\phi+\theta}{2}\right) + y \sin\left(\frac{\phi+\theta}{2}\right) = \cos\left(\frac{\theta - \phi}{2}\right)$.
In the normal form $x \cos \alpha + y \sin \alpha = p$, the distance from the origin is $|p|$.
Distance $= \left|\cos\left(\frac{\theta - \phi}{2}\right)\right|$
Since $\cos(-x) = \cos x$, we have $\cos\left(\frac{\theta - \phi}{2}\right) = \cos\left(\frac{\phi - \theta}{2}\right)$.
Distance $= \left|\cos\left(\frac{\phi - \theta}{2}\right)\right|$
Both methods yield the same result. The perpendicular distance from the origin to the line joining the points $(\cos \theta, \sin \theta)$ and $(\cos \phi, \sin \phi)$ is $\left|\cos\left(\frac{\phi - \theta}{2}\right)\right|$.
Question 6. Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.
Answer:
Given:
Equation of the first line: $L_1: x - 7y + 5 = 0$.
Equation of the second line: $L_2: 3x + y = 0$.
A required line which is parallel to the y-axis and passes through the intersection of $L_1$ and $L_2$.
To Find:
The equation of the required line.
Solution:
Let the point of intersection of the lines $L_1$ and $L_2$ be $(x, y)$. This point satisfies both equations.
We have the system of equations:
$x - 7y + 5 = 0$
... (i)
$3x + y = 0$
... (ii)
From equation (ii), we can express $y$ in terms of $x$:
$y = -3x$
From (ii)
Substitute this expression for $y$ into equation (i):
$x - 7(-3x) + 5 = 0$
Substitute $y$ into (i)
$x + 21x + 5 = 0$
$22x + 5 = 0$
$22x = -5$
$x = -\frac{5}{22}$
x-coordinate of intersection
Now substitute the value of $x$ back into the expression for $y$ ($y = -3x$):
$y = -3\left(-\frac{5}{22}\right)$
Substitute $x$ value
$y = \frac{15}{22}$
y-coordinate of intersection
The point of intersection of the two lines is $\left(-\frac{5}{22}, \frac{15}{22}\right)$.
A line parallel to the y-axis has an equation of the form $x = k$, where $k$ is a constant.
Since the required line passes through the point of intersection $\left(-\frac{5}{22}, \frac{15}{22}\right)$, the x-coordinate of this point must satisfy the equation $x = k$.
$k = -\frac{5}{22}$
Therefore, the equation of the line parallel to the y-axis and passing through the intersection point is:
$x = -\frac{5}{22}$
We can rewrite this equation in the general form by multiplying by 22 and rearranging:
$22x = -5$
$22x + 5 = 0$
Equation of the required line
The equation of the line is $22x + 5 = 0$.
Question 7. Find the equation of a line drawn perpendicular to the line $\frac{x}{4}$ + $\frac{y}{6}$ =1 through the point, where it meets the y-axis.
Answer:
Given:
The equation of a line: $\frac{x}{4} + \frac{y}{6} = 1$.
A required line is perpendicular to the given line and passes through the point where the given line meets the y-axis.
To Find:
The equation of the required line.
Solution:
First, let's find the point where the given line intersects the y-axis. This point is the y-intercept, and the x-coordinate is 0.
Substitute $x = 0$ into the equation $\frac{x}{4} + \frac{y}{6} = 1$:
$\frac{0}{4} + \frac{y}{6} = 1$
Substitute $x=0$
$0 + \frac{y}{6} = 1$
$\frac{y}{6} = 1$
$y = 6$
y-coordinate of intersection
The given line meets the y-axis at the point $(0, 6)$. The required line passes through this point.
Next, let's find the slope of the given line $\frac{x}{4} + \frac{y}{6} = 1$. Convert the equation to the slope-intercept form $y = mx + c$:
$\frac{y}{6} = 1 - \frac{x}{4}$
$y = 6\left(1 - \frac{x}{4}\right)$
Multiply by 6
$y = 6 - \frac{6x}{4}$
$y = -\frac{3}{2}x + 6$
Slope-intercept form
The slope of the given line is $m_1 = -\frac{3}{2}$.
The required line is perpendicular to the given line. If $m_1$ is the slope of the given line and $m_2$ is the slope of the perpendicular line, then the product of their slopes is $-1$, provided neither line is vertical or horizontal.
$m_1 \times m_2 = -1$
Perpendicular slopes condition
$\left(-\frac{3}{2}\right) \times m_2 = -1$
$m_2 = \frac{-1}{-\frac{3}{2}}$
$m_2 = \frac{2}{3}$
Slope of the required line
Now, we have the slope of the required line ($m = \frac{2}{3}$) and a point it passes through ($(x_1, y_1) = (0, 6)$).
Using the point-slope form of the equation of a line, $y - y_1 = m(x - x_1)$:
$y - 6 = \frac{2}{3}(x - 0)$
Point-slope form with $(0,6)$ and $m=2/3$
$y - 6 = \frac{2}{3}x$
Multiply the equation by 3 to clear the denominator:
$3(y - 6) = 3 \times \frac{2}{3}x$
Multiply by 3
$3y - 18 = 2x$
Rearrange the equation to the general form $Ax + By + C = 0$:
$2x - 3y + 18 = 0$
Equation of the required line
The equation of the line perpendicular to $\frac{x}{4} + \frac{y}{6} = 1$ and passing through its y-intercept is $2x - 3y + 18 = 0$.
Question 8. Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
Answer:
Given:
The equations of three lines:
$L_1: y - x = 0 \implies y = x$
$L_2: x + y = 0 \implies y = -x$
$L_3: x - k = 0 \implies x = k$
We assume $k \neq 0$, otherwise, all three lines pass through the origin and do not form a triangle.
To Find:
The area of the triangle formed by these three lines.
Solution:
To find the area of the triangle, we determine the coordinates of its vertices by finding the intersection points of the lines pairwise.
Vertex 1: Intersection of $L_1$ ($y = x$) and $L_2$ ($y = -x$)
Set the y-values equal:
$x = -x$
$2x = 0$
$x = 0$
Substitute $x = 0$ into $y = x$:
$y = 0$
The first vertex is $A(0, 0)$ (the origin).
Vertex 2: Intersection of $L_1$ ($y = x$) and $L_3$ ($x = k$)
Substitute $x = k$ into the equation $y = x$:
$y = k$
The second vertex is $B(k, k)$.
Vertex 3: Intersection of $L_2$ ($y = -x$) and $L_3$ ($x = k$)
Substitute $x = k$ into the equation $y = -x$:
$y = -k$
The third vertex is $C(k, -k)$.
The three vertices of the triangle are $A(0, 0)$, $B(k, k)$, and $C(k, -k)$.
We can calculate the area of the triangle using the coordinates of the vertices. The area of a triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$, and $(x_3, y_3)$ is given by:
Area $= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$
Area formula using coordinates
Substitute the coordinates of $A(0, 0)$, $B(k, k)$, and $C(k, -k)$ into the formula:
Area $= \frac{1}{2} |0(k - (-k)) + k(-k - 0) + k(0 - k)|$
Area $= \frac{1}{2} |0(2k) + k(-k) + k(-k)|$
Area $= \frac{1}{2} |0 - k^2 - k^2|$
Area $= \frac{1}{2} |-2k^2|$
Area $= \frac{1}{2} \times 2|k^2|$
Since $k^2 \ge 0$, $|k^2| = k^2$.
Area $= k^2$
Alternatively, we can use the base and height method.
The base of the triangle can be taken as the line segment BC, which lies on the vertical line $x = k$. The length of the base is the distance between points $B(k, k)$ and $C(k, -k)$.
Base length $= \sqrt{(k - k)^2 + (-k - k)^2}$
Distance formula
Base length $= \sqrt{0^2 + (-2k)^2}$
Base length $= \sqrt{4k^2}$
Base length $= |2k|$
Length of base BC
The height of the triangle is the perpendicular distance from the vertex A $(0, 0)$ to the base BC (the line $x = k$ or $x - k = 0$).
The distance of a point $(x_0, y_0)$ from the line $Ax + By + C = 0$ is $\frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$.
Here, $(x_0, y_0) = (0, 0)$ and the line is $x - k = 0$ ($A=1, B=0, C=-k$).
Height $= \frac{|1(0) + 0(0) - k|}{\sqrt{1^2 + 0^2}}$
Distance from origin to $x=k$
Height $= \frac{|-k|}{\sqrt{1}}$
Height $= |k|$
Height of the triangle
The area of the triangle is $\frac{1}{2} \times \text{base} \times \text{height}$.
Area $= \frac{1}{2} \times |2k| \times |k|$
Area $= \frac{1}{2} \times 2|k| \times |k|$
Area $= |k|^2$
Since $|k|^2 = k^2$:
Area $= k^2$
The area of the triangle formed by the given lines is $k^2$. Note that the area is always non-negative, which is consistent with $|k^2| = k^2$. If $k=0$, the lines intersect at the origin, and the area of the degenerate triangle is 0, which is $0^2$.
Question 9. Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
Answer:
Given:
Three lines with equations:
$L_1: 3x + y - 2 = 0$
$L_2: px + 2y - 3 = 0$
$L_3: 2x - y - 3 = 0$
To Find:
The value of $p$ such that the three lines intersect at one point (are concurrent).
Solution:
For three lines to intersect at one point, the intersection point of any two lines must lie on the third line.
Let's find the intersection point of lines $L_1$ and $L_3$. We have the system of equations:
$3x + y = 2$
... (i)
$2x - y = 3$
... (ii)
We can solve this system by elimination. Add equation (i) and equation (ii):
$(3x + y) + (2x - y) = 2 + 3$
$5x = 5$
$x = 1$
x-coordinate of intersection
Substitute the value of $x = 1$ into equation (i) to find $y$:
$3(1) + y = 2$
Substitute $x=1$ into (i)
$3 + y = 2$
$y = 2 - 3$
$y = -1$
y-coordinate of intersection
The intersection point of lines $L_1$ and $L_3$ is $(1, -1)$.
For the three lines to intersect at one point, this intersection point $(1, -1)$ must lie on the third line $L_2$ ($px + 2y - 3 = 0$).
Substitute the coordinates $(1, -1)$ into the equation of $L_2$:
$p(1) + 2(-1) - 3 = 0$
Point $(1,-1)$ satisfies $L_2$
$p - 2 - 3 = 0$
$p - 5 = 0$
$p = 5$
Value of p
Therefore, the value of $p$ for which the three lines intersect at one point is $5$.
Alternate Solution (Using Determinant):
Three lines $A_1x + B_1y + C_1 = 0$, $A_2x + B_2y + C_2 = 0$, and $A_3x + B_3y + C_3 = 0$ are concurrent if and only if the determinant of their coefficients is zero:
$\begin{vmatrix} A_1 & B_1 & C_1 \\ A_2 & B_2 & C_2 \\ A_3 & B_3 & C_3 \end{vmatrix} = 0$
Concurrency condition
For the given lines:
$L_1: 3x + y - 2 = 0 \implies A_1=3, B_1=1, C_1=-2$
$L_2: px + 2y - 3 = 0 \implies A_2=p, B_2=2, C_2=-3$
$L_3: 2x - y - 3 = 0 \implies A_3=2, B_3=-1, C_3=-3$
Set the determinant of the coefficients to zero:
$\begin{vmatrix} 3 & 1 & -2 \\ p & 2 & -3 \\ 2 & -1 & -3 \end{vmatrix} = 0$
Expand the determinant along the first row:
$3 \begin{vmatrix} 2 & -3 \\ -1 & -3 \end{vmatrix} - 1 \begin{vmatrix} p & -3 \\ 2 & -3 \end{vmatrix} + (-2) \begin{vmatrix} p & 2 \\ 2 & -1 \end{vmatrix} = 0$
$3((2)(-3) - (-3)(-1)) - 1((p)(-3) - (-3)(2)) - 2((p)(-1) - (2)(2)) = 0$
$3(-6 - 3) - 1(-3p + 6) - 2(-p - 4) = 0$
$3(-9) - (-3p + 6) - (-2p - 8) = 0$
$-27 + 3p - 6 + 2p + 8 = 0$
$(3p + 2p) + (-27 - 6 + 8) = 0$
$5p - 25 = 0$
$5p = 25$
$p = 5$
Value of p from determinant
Both methods yield the same result. The value of $p$ is $5$.
Question 10. If three lines whose equations are y = m1x + c1 , y = m2x + c2 and y = m3x + c3 are concurrent, then show that m1(c2 – c3) + m2(c3 – c1) + m3(c1 – c2) = 0.
Answer:
Given:
Three lines with equations in slope-intercept form:
$L_1: y = m_1x + c_1$
$L_2: y = m_2x + c_2$
$L_3: y = m_3x + c_3$
The lines are concurrent, meaning they intersect at a single point.
To Show:
The condition for concurrency is $m_1(c_2 – c_3) + m_2(c_3 – c_1) + m_3(c_1 – c_2) = 0$.
Solution:
For the three lines to be concurrent, the point of intersection of any two lines must lie on the third line.
Let's find the point of intersection of lines $L_1$ ($y = m_1x + c_1$) and $L_2$ ($y = m_2x + c_2$).
At the intersection point, the y-coordinates are equal:
$m_1x + c_1 = m_2x + c_2$
Equating y-values of $L_1, L_2$
Rearrange the equation to solve for $x$:
$m_1x - m_2x = c_2 - c_1$
$(m_1 - m_2)x = c_2 - c_1$
Assuming $m_1 \neq m_2$ (if $m_1 = m_2$, the lines $L_1$ and $L_2$ are parallel; for concurrent lines, they must then be the same line or $m_3$ must be equal to $m_1$ and the lines must all be the same, which the final condition handles), we can write:
$x = \frac{c_2 - c_1}{m_1 - m_2}$
x-coordinate of intersection
Now, substitute this value of $x$ back into the equation for $L_1$ (or $L_2$) to find the corresponding $y$-coordinate:
$y = m_1\left(\frac{c_2 - c_1}{m_1 - m_2}\right) + c_1$
Substitute x-coordinate into $L_1$
$y = \frac{m_1(c_2 - c_1) + c_1(m_1 - m_2)}{m_1 - m_2}$
$y = \frac{m_1c_2 - m_1c_1 + c_1m_1 - c_1m_2}{m_1 - m_2}$
$y = \frac{m_1c_2 - c_1m_2}{m_1 - m_2}$
y-coordinate of intersection
The point of intersection of $L_1$ and $L_2$ is $\left(\frac{c_2 - c_1}{m_1 - m_2}, \frac{m_1c_2 - c_1m_2}{m_1 - m_2}\right)$.
For the three lines to be concurrent, this point must also lie on the third line $L_3$ ($y = m_3x + c_3$). Substitute the coordinates of the intersection point into the equation of $L_3$:
$\frac{m_1c_2 - c_1m_2}{m_1 - m_2} = m_3\left(\frac{c_2 - c_1}{m_1 - m_2}\right) + c_3$
Intersection point satisfies $L_3$
Multiply both sides of the equation by $(m_1 - m_2)$ (assuming $m_1 \neq m_2$):
$m_1c_2 - c_1m_2 = m_3(c_2 - c_1) + c_3(m_1 - m_2)$
$m_1c_2 - c_1m_2 = m_3c_2 - m_3c_1 + c_3m_1 - c_3m_2$
Rearrange the terms to group them according to the slopes $m_1$, $m_2$, and $m_3$. Move all terms to one side:
$m_1c_2 - c_1m_2 - m_3c_2 + m_3c_1 - c_3m_1 + c_3m_2 = 0$
Group terms with $m_1$, $m_2$, and $m_3$:
$(m_1c_2 - c_3m_1) + (-c_1m_2 + c_3m_2) + (-m_3c_2 + m_3c_1) = 0$
Factor out $m_1$, $m_2$, and $m_3$ from their respective groups:
$m_1(c_2 - c_3) + m_2(c_3 - c_1) + m_3(c_1 - c_2) = 0$
The required condition
This condition is valid even when $m_1 = m_2$ or other slopes are equal, as shown by the equivalent determinant condition for concurrency of $A_ix + B_iy + C_i = 0$ lines, where $A_i=m_i, B_i=-1, C_i=c_i$.
Thus, if the three lines $y = m_1x + c_1$, $y = m_2x + c_2$, and $y = m_3x + c_3$ are concurrent, then $m_1(c_2 – c_3) + m_2(c_3 – c_1) + m_3(c_1 – c_2) = 0$.
Question 11. Find the equation of the lines through the point (3, 2) which make an angle of 45° with the line x – 2y = 3.
Answer:
Given:
Point $P(3, 2)$.
The equation of the line: $L_1: x - 2y = 3$.
The required lines make an angle of $45^\circ$ with the given line.
To Find:
The equations of the lines passing through $(3, 2)$ and making an angle of $45^\circ$ with the line $x - 2y = 3$.
Solution:
First, find the slope of the given line $L_1$. Rewrite the equation $x - 2y = 3$ in the slope-intercept form $y = mx + c$.
$-2y = -x + 3$
Rearranging $L_1$ equation
$y = \frac{-x + 3}{-2}$
$y = \frac{1}{2}x - \frac{3}{2}$
Slope-intercept form
The slope of the given line $L_1$ is $m_1 = \frac{1}{2}$.
Let $m$ be the slope of the required line. The angle $\alpha$ between two lines with slopes $m_1$ and $m$ is given by the formula:
$\tan \alpha = \left|\frac{m - m_1}{1 + m m_1}\right|$
Angle between lines formula
We are given that the angle is $\alpha = 45^\circ$, and $\tan 45^\circ = 1$. Substitute the values $m_1 = \frac{1}{2}$ and $\alpha = 45^\circ$ into the formula:
$1 = \left|\frac{m - \frac{1}{2}}{1 + m \left(\frac{1}{2}\right)}\right|$
$1 = \left|\frac{\frac{2m - 1}{2}}{\frac{2 + m}{2}}\right|$
$1 = \left|\frac{2m - 1}{2 + m}\right|$
This absolute value equation gives two possibilities:
Case 1: $\frac{2m - 1}{2 + m} = 1$
$2m - 1 = 1 \times (2 + m)$
$2m - 1 = 2 + m$
$2m - m = 2 + 1$
$m = 3$
Slope for the first line
Case 2: $\frac{2m - 1}{2 + m} = -1$
$2m - 1 = -1 \times (2 + m)$
$2m - 1 = -2 - m$
$2m + m = -2 + 1$
$3m = -1$
$m = -\frac{1}{3}$
Slope for the second line
We have two possible slopes for the required lines: $m_2 = 3$ and $m_3 = -\frac{1}{3}$. Both lines pass through the point $(3, 2)$.
Use the point-slope form of the equation of a line, $y - y_0 = m(x - x_0)$, with $(x_0, y_0) = (3, 2)$.
Equation of the first line (with slope $m_2 = 3$):
$y - 2 = 3(x - 3)$
$y - 2 = 3x - 9$
Rearrange to the general form:
$3x - y - 9 + 2 = 0$
$3x - y - 7 = 0$
Equation of the first line
Equation of the second line (with slope $m_3 = -\frac{1}{3}$):
$y - 2 = -\frac{1}{3}(x - 3)$
Multiply by 3 to clear the denominator:
$3(y - 2) = -1(x - 3)$
$3y - 6 = -x + 3$
Rearrange to the general form:
$x + 3y - 6 - 3 = 0$
$x + 3y - 9 = 0$
Equation of the second line
The equations of the two lines are $3x - y - 7 = 0$ and $x + 3y - 9 = 0$.
Question 12. Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.
Answer:
Given:
Equation of the first line: $L_1: 4x + 7y - 3 = 0$.
Equation of the second line: $L_2: 2x - 3y + 1 = 0$.
A required line passes through the intersection of $L_1$ and $L_2$ and has equal intercepts on the axes.
To Find:
The equation of the required line.
Solution:
First, find the point of intersection of lines $L_1$ and $L_2$. We have the system of equations:
$4x + 7y = 3$
... (i)
$2x - 3y = -1$
... (ii)
Multiply equation (ii) by 2 to make the coefficient of $x$ the same as in equation (i):
$2 \times (2x - 3y) = 2 \times (-1)$
$4x - 6y = -2$
... (iii)
Subtract equation (iii) from equation (i):
$(4x + 7y) - (4x - 6y) = 3 - (-2)$
$4x + 7y - 4x + 6y = 3 + 2$
$13y = 5$
$y = \frac{5}{13}$
y-coordinate of intersection
Substitute the value of $y = \frac{5}{13}$ into equation (ii) to find $x$:
$2x - 3\left(\frac{5}{13}\right) = -1$
Substitute $y$ into (ii)
$2x - \frac{15}{13} = -1$
$2x = -1 + \frac{15}{13}$
$2x = \frac{-13 + 15}{13}$
$2x = \frac{2}{13}$
$x = \frac{1}{13}$
x-coordinate of intersection
The point of intersection of the two lines is $\left(\frac{1}{13}, \frac{5}{13}\right)$. The required line passes through this point.
Let the equation of the required line be in the intercept form $\frac{x}{a} + \frac{y}{b} = 1$.
We are given that the line has equal intercepts on the axes, which means $a = b$.
So the equation becomes $\frac{x}{a} + \frac{y}{a} = 1$.
Multiply by $a$ to get $x + y = a$. Rearranging, we get $x + y - a = 0$.
This line passes through the point of intersection $\left(\frac{1}{13}, \frac{5}{13}\right)$. Substitute these coordinates into the equation $x + y - a = 0$:
$\frac{1}{13} + \frac{5}{13} - a = 0$
Intersection point satisfies the required line equation
$\frac{1 + 5}{13} - a = 0$
$\frac{6}{13} - a = 0$
$a = \frac{6}{13}$
Value of the equal intercept
Since $a = b$, the equation of the required line is $\frac{x}{6/13} + \frac{y}{6/13} = 1$.
$\frac{13x}{6} + \frac{13y}{6} = 1$
Multiply by 6:
$13x + 13y = 6$
Rearranging to the general form:
$13x + 13y - 6 = 0$
Equation of the required line
Alternatively, we can directly use the equation $x+y=a$ and substitute the intersection point.
$\frac{1}{13} + \frac{5}{13} = a$
$a = \frac{6}{13}$
The equation is $x + y = \frac{6}{13}$.
Multiply by 13:
$13x + 13y = 6$
$13x + 13y - 6 = 0$
Equation using alternate method
The equation of the line is $13x + 13y - 6 = 0$.
Question 13. Show that the equation of the line passing through the origin and making an angle θ with the line y = mx + c is $\frac{y}{x} = \frac{m \;\pm\; tan \;θ}{1 \;\mp\; m tan \;θ}$ .
Answer:
Given:
Equation of line 1: $L_1: y = mx + c$.
A required line $L_2$ passes through the origin $(0, 0)$.
The angle between $L_1$ and $L_2$ is $\theta$.
To Show:
The equation of line $L_2$ is $\frac{y}{x} = \frac{m \;\pm\; tan \;θ}{1 \;\mp\; m tan \;θ}$.
Solution:
The equation of the given line $L_1$ is $y = mx + c$. The slope of $L_1$ is $m_1 = m$.
The required line $L_2$ passes through the origin $(0, 0)$. Any line passing through the origin (except the y-axis) can be represented by the equation $y = m_2x$, where $m_2$ is the slope of $L_2$.
The angle $\alpha$ between two lines with slopes $m_1$ and $m_2$ is given by the formula:
$\tan \alpha = \left|\frac{m_2 - m_1}{1 + m_1 m_2}\right|$
Formula for angle between lines
In this problem, the angle between $L_1$ and $L_2$ is $\theta$, and the slope of $L_1$ is $m_1 = m$. Substitute these into the formula:
$\tan \theta = \left|\frac{m_2 - m}{1 + m m_2}\right|$
Applying the formula
This absolute value equation leads to two possibilities:
Case 1: $\frac{m_2 - m}{1 + m m_2} = \tan \theta$
Assuming $1 + m m_2 \neq 0$, multiply both sides by $(1 + m m_2)$:
$m_2 - m = \tan \theta (1 + m m_2)$
$m_2 - m = \tan \theta + m m_2 \tan \theta$
Rearrange the terms to group $m_2$ on one side:
$m_2 - m m_2 \tan \theta = m + \tan \theta$
Factor out $m_2$:
$m_2 (1 - m \tan \theta) = m + \tan \theta$
Assuming $1 - m \tan \theta \neq 0$, solve for $m_2$:
$m_2 = \frac{m + \tan \theta}{1 - m \tan \theta}$
Slope for Case 1
Case 2: $\frac{m_2 - m}{1 + m m_2} = -\tan \theta$
Assuming $1 + m m_2 \neq 0$, multiply both sides by $(1 + m m_2)$:
$m_2 - m = -\tan \theta (1 + m m_2)$
$m_2 - m = -\tan \theta - m m_2 \tan \theta$
Rearrange the terms to group $m_2$ on one side:
$m_2 + m m_2 \tan \theta = m + \tan \theta - \tan \theta - (-\tan \theta)$
$m_2 + m m_2 \tan \theta = m - \tan \theta$
Factor out $m_2$:
$m_2 (1 + m \tan \theta) = m - \tan \theta$
Assuming $1 + m \tan \theta \neq 0$, solve for $m_2$:
$m_2 = \frac{m - \tan \theta}{1 + m \tan \theta}$
Slope for Case 2
The slope $m_2$ of the required line is either $\frac{m + \tan \theta}{1 - m \tan \theta}$ or $\frac{m - \tan \theta}{1 + m \tan \theta}$. These two possibilities can be expressed using the $\pm$ and $\mp$ notation:
$m_2 = \frac{m \pm \tan \theta}{1 \mp m \tan \theta}$
Combined slopes
Since the required line passes through the origin and has slope $m_2$, its equation is $y = m_2x$. For any point $(x, y)$ on this line other than the origin (where $x \neq 0$), we can write $m_2 = \frac{y}{x}$.
Substitute $\frac{y}{x}$ for $m_2$ in the expression for the slope:
$\frac{y}{x} = \frac{m \;\pm\; tan \;θ}{1 \;\mp\; m tan \;θ}$
This is the required equation of the line passing through the origin and making an angle $\theta$ with the line $y = mx + c$. This derivation is valid when $\tan \theta$ is defined and the denominators $1 \mp m \tan \theta$ are non-zero.
Question 14. In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line x + y = 4?
Answer:
Given:
Point 1: $A(-1, 1)$.
Point 2: $B(5, 7)$.
Dividing line: $L: x + y = 4$.
To Find:
The ratio in which the line segment joining points $A$ and $B$ is divided by the line $x + y = 4$.
Solution:
Let the line joining points $A(-1, 1)$ and $B(5, 7)$ be divided by the line $x + y = 4$ at a point $P(x, y)$ in the ratio $\lambda : 1$.
Using the section formula, the coordinates of point $P$ that divides the line segment joining $(x_1, y_1)$ and $(x_2, y_2)$ in the ratio $\lambda : 1$ are given by:
$x = \frac{\lambda x_2 + 1 x_1}{\lambda + 1}$
$y = \frac{\lambda y_2 + 1 y_1}{\lambda + 1}$
Section formula
Here, $(x_1, y_1) = (-1, 1)$ and $(x_2, y_2) = (5, 7)$. The coordinates of $P$ are:
$x = \frac{\lambda(5) + 1(-1)}{\lambda + 1} = \frac{5\lambda - 1}{\lambda + 1}$
$y = \frac{\lambda(7) + 1(1)}{\lambda + 1} = \frac{7\lambda + 1}{\lambda + 1}$
Coordinates of point P in terms of $\lambda$
Since the point $P(x, y)$ lies on the line $x + y = 4$, its coordinates must satisfy the equation of the line.
Substitute the expressions for $x$ and $y$ into the equation $x + y = 4$:
$\left(\frac{5\lambda - 1}{\lambda + 1}\right) + \left(\frac{7\lambda + 1}{\lambda + 1}\right) = 4$
Point P satisfies the line equation
Combine the fractions on the left side:
$\frac{(5\lambda - 1) + (7\lambda + 1)}{\lambda + 1} = 4$
$\frac{5\lambda - 1 + 7\lambda + 1}{\lambda + 1} = 4$
$\frac{12\lambda}{\lambda + 1} = 4$
Assuming $\lambda + 1 \neq 0$ (i.e., $\lambda \neq -1$, which would mean the point is at infinity), multiply both sides by $(\lambda + 1)$:
$12\lambda = 4(\lambda + 1)$
$12\lambda = 4\lambda + 4$
Rearrange the terms to solve for $\lambda$:
$12\lambda - 4\lambda = 4$
$8\lambda = 4$
$\lambda = \frac{4}{8}$
$\lambda = \frac{1}{2}$
Value of lambda
The ratio is $\lambda : 1 = \frac{1}{2} : 1$.
To express this as a ratio of integers, multiply both parts by 2:
$\frac{1}{2} \times 2 : 1 \times 2$
$1 : 2$
The required ratio
Since $\lambda$ is positive, the point of intersection $P$ lies between $A$ and $B$, dividing the segment internally.
The line joining points $(-1, 1)$ and $(5, 7)$ is divided by the line $x + y = 4$ in the ratio $1 : 2$.
Question 15. Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y = 0.
Answer:
Given:
Point $P(1, 2)$.
Line 1 ($L_1$): $4x + 7y + 5 = 0$.
Line 2 ($L_2$, the direction line): $2x - y = 0$.
To Find:
The distance of line $L_1$ from point $P(1, 2)$ measured along line $L_2$.
Solution:
The distance of the line $4x + 7y + 5 = 0$ from the point $(1, 2)$ measured along the line $2x - y = 0$ is the distance between the point $(1, 2)$ and the point of intersection of the two lines $4x + 7y + 5 = 0$ and $2x - y = 0$.
Let $Q(x, y)$ be the point of intersection of the lines $4x + 7y + 5 = 0$ and $2x - y = 0$. We need to solve the following system of equations:
$4x + 7y = -5$
... (i)
$2x - y = 0$
... (ii)
From equation (ii), we can express $y$ in terms of $x$:
$y = 2x$
From (ii)
Substitute this expression for $y$ into equation (i):
$4x + 7(2x) = -5$
Substitute $y$ into (i)
$4x + 14x = -5$
$18x = -5$
$x = -\frac{5}{18}$
x-coordinate of Q
Now substitute the value of $x$ back into the expression for $y$ ($y = 2x$):
$y = 2\left(-\frac{5}{18}\right)$
Substitute $x$ value
$y = -\frac{10}{18}$
$y = -\frac{5}{9}$
y-coordinate of Q
The point of intersection $Q$ is $\left(-\frac{5}{18}, -\frac{5}{9}\right)$.
The required distance is the distance between the point $P(1, 2)$ and the point $Q\left(-\frac{5}{18}, -\frac{5}{9}\right)$.
Using the distance formula between two points $(x_1, y_1)$ and $(x_2, y_2)$, which is $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$:
Distance $PQ = \sqrt{\left(-\frac{5}{18} - 1\right)^2 + \left(-\frac{5}{9} - 2\right)^2}$
Using distance formula
Distance $PQ = \sqrt{\left(-\frac{5}{18} - \frac{18}{18}\right)^2 + \left(-\frac{5}{9} - \frac{18}{9}\right)^2}$
Distance $PQ = \sqrt{\left(-\frac{23}{18}\right)^2 + \left(-\frac{23}{9}\right)^2}$
Distance $PQ = \sqrt{\left(\frac{23}{18}\right)^2 + \left(\frac{2 \times 23}{18}\right)^2}$
Distance $PQ = \sqrt{\frac{23^2}{18^2} + \frac{4 \times 23^2}{18^2}}$
Distance $PQ = \sqrt{\frac{23^2 (1 + 4)}{18^2}}$
Distance $PQ = \sqrt{\frac{23^2 \times 5}{18^2}}$
Distance $PQ = \frac{\sqrt{23^2} \times \sqrt{5}}{\sqrt{18^2}}$
Distance $PQ = \frac{23\sqrt{5}}{18}$
The distance of the line $4x + 7y + 5 = 0$ from the point $(1, 2)$ measured along the line $2x - y = 0$ is $\frac{23\sqrt{5}}{18}$ units.
Question 16. Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point.
Answer:
Given:
Point $P(-1, 2)$.
Line $L_1: x + y = 4$.
The distance from point $P$ to the point of intersection with line $L_1$ is $d = 3$ units.
To Find:
The direction (slope or angle) of the straight line drawn through $P(-1, 2)$.
Solution:
Let the required straight line pass through the point $P(-1, 2)$. Let $Q(x, y)$ be the point of intersection of this required line and the line $x + y = 4$.
The point $Q(x, y)$ lies on the line $x + y = 4$. Thus, its coordinates satisfy the equation:
$x + y = 4$
Q lies on the line $L_1$
The distance between the point $P(-1, 2)$ and the point $Q(x, y)$ is given as 3 units. Using the distance formula:
$\sqrt{(x - (-1))^2 + (y - 2)^2} = 3$
Distance PQ is 3 units
Squaring both sides of the equation:
$(x + 1)^2 + (y - 2)^2 = 3^2$
$(x + 1)^2 + (y - 2)^2 = 9$
... (i)
From the equation of line $L_1$, we can express $y$ in terms of $x$:
$y = 4 - x$
From $x+y=4$
Substitute this expression for $y$ into equation (i):
$(x + 1)^2 + ((4 - x) - 2)^2 = 9$
Substitute $y$ into (i)
$(x + 1)^2 + (2 - x)^2 = 9$
Expand and simplify the equation:
$(x^2 + 2x + 1) + (4 - 4x + x^2) = 9$
$x^2 + 2x + 1 + 4 - 4x + x^2 = 9$
$2x^2 - 2x + 5 = 9$
$2x^2 - 2x - 4 = 0$
Quadratic equation for x
Divide the quadratic equation by 2:
$x^2 - x - 2 = 0$
Factor the quadratic equation:
$(x - 2)(x + 1) = 0$
This gives two possible values for the x-coordinate of the intersection point $Q$:
$x = 2$ or $x = -1$
Possible x-coordinates for Q
Now find the corresponding y-coordinates using the equation $y = 4 - x$:
Case 1: If $x = 2$
$y = 4 - 2 = 2$
The first possible intersection point is $Q_1(2, 2)$.
Case 2: If $x = -1$
$y = 4 - (-1) = 4 + 1 = 5$
The second possible intersection point is $Q_2(-1, 5)$.
The required straight line passes through the point $P(-1, 2)$ and one of these intersection points, $Q_1$ or $Q_2$. The direction of the line is given by the slope of the line segment $PQ$.
Direction 1: The line passes through $P(-1, 2)$ and $Q_1(2, 2)$.
The slope $m_1$ of the line passing through $(x_P, y_P) = (-1, 2)$ and $(x_1, y_1) = (2, 2)$ is:
$m_1 = \frac{y_1 - y_P}{x_1 - x_P} = \frac{2 - 2}{2 - (-1)}$
Slope formula
$m_1 = \frac{0}{3} = 0$
Slope of the first line
A line with slope 0 is a horizontal line. This corresponds to a direction parallel to the x-axis.
Direction 2: The line passes through $P(-1, 2)$ and $Q_2(-1, 5)$.
The slope $m_2$ of the line passing through $(x_P, y_P) = (-1, 2)$ and $(x_2, y_2) = (-1, 5)$ is:
$m_2 = \frac{y_2 - y_P}{x_2 - x_P} = \frac{5 - 2}{-1 - (-1)}$
Slope formula
$m_2 = \frac{3}{0}$
Slope of the second line
A slope of $\frac{3}{0}$ is undefined. This indicates a vertical line. This corresponds to a direction parallel to the y-axis.
The directions in which a straight line must be drawn through the point $(-1, 2)$ are given by the slopes $0$ and undefined. These directions correspond to the horizontal line $y=2$ and the vertical line $x=-1$ passing through $P(-1,2)$.
Question 17. The hypotenuse of a right angled triangle has its ends at the points (1, 3) and (– 4, 1). Find an equation of the legs (perpendicular sides) of the triangle.
Answer:
Given:
The endpoints of the hypotenuse of a right-angled triangle are $A(1, 3)$ and $B(-4, 1)$.
To Find:
An equation of the legs (perpendicular sides) of the triangle.
Solution:
Let the third vertex of the right-angled triangle, where the right angle is formed, be $C$. The legs of the triangle are the lines containing the segments $AC$ and $BC$.
Since the angle at $C$ is a right angle, the line containing segment $AC$ is perpendicular to the line containing segment $BC$.
Let the equation of one leg passing through point $A(1, 3)$ be represented in the general form $A'(x - x_1) + B'(y - y_1) = 0$. For point $A(1, 3)$, this is:
$A(x - 1) + B(y - 3) = 0$
Equation of a line through A ... (i)
where $A$ and $B$ are arbitrary real constants, not both zero.
Let the equation of the other leg passing through point $B(-4, 1)$ be $L_2$. Since $L_2$ is perpendicular to the first leg, its equation must be of a form that represents a line perpendicular to $A(x - 1) + B(y - 3) = 0$ and passing through $B(-4, 1)$.
The general form of a line perpendicular to $Ax + By + C = 0$ is $Bx - Ay + C' = 0$. Similarly, a line perpendicular to $A(x - x_0) + B(y - y_0) = 0$ passing through $(x_1, y_1)$ has the form $B(x - x_1) - A(y - y_1) = 0$.
Applying this for the second leg passing through $B(-4, 1)$ and perpendicular to the line $A(x - 1) + B(y - 3) = 0$, its equation is:
$B(x - (-4)) - A(y - 1) = 0$
Perpendicular line through B
$B(x + 4) - A(y - 1) = 0$
Equation of the other leg ... (ii)
where $A$ and $B$ are the same constants as in equation (i).
For any real values of $A$ and $B$, as long as they are not both zero, the two equations $A(x - 1) + B(y - 3) = 0$ and $B(x + 4) - A(y - 1) = 0$ represent a pair of perpendicular lines passing through $A(1, 3)$ and $B(-4, 1)$ respectively. The intersection of these two lines gives the vertex $C$ where the right angle is located, thus forming a right-angled triangle with hypotenuse $AB$.
Thus, the equations of the legs of the triangle are given by the pair of equations:
$A(x - 1) + B(y - 3) = 0$
$B(x + 4) - A(y - 1) = 0$
where $A, B \in \mathbb{R}$ are arbitrary constants, not both zero.
Question 18. Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Answer:
Given:
Point $P(3, 8)$.
Line $L$ (acting as a plane mirror) with equation $x + 3y = 7$, or $x + 3y - 7 = 0$ in general form.
To Find:
The image of the point $P(3, 8)$ with respect to the line $x + 3y = 7$.
Solution:
Let the image of the point $P(3, 8)$ in the line $x + 3y - 7 = 0$ be the point $Q(x', y')$.
For $Q$ to be the image of $P$ in the line $L$, two geometric conditions must hold:
1. The line segment $PQ$ is perpendicular to the mirror line $L$.
2. The midpoint of the line segment $PQ$ lies on the mirror line $L$.
First, let's find the slope of the mirror line $L$. The equation is $x + 3y = 7$.
$3y = -x + 7$
$y = -\frac{1}{3}x + \frac{7}{3}$
The slope of the mirror line $L$ is $m_L = -\frac{1}{3}$.
The slope of the line segment $PQ$ joining $P(3, 8)$ and $Q(x', y')$ is $m_{PQ} = \frac{y' - 8}{x' - 3}$.
Since $PQ$ is perpendicular to $L$, the product of their slopes is $-1$.
$m_{PQ} \times m_L = -1$
Perpendicularity condition
$\left(\frac{y' - 8}{x' - 3}\right) \times \left(-\frac{1}{3}\right) = -1$
$\frac{y' - 8}{x' - 3} = 3$
$y' - 8 = 3(x' - 3)$
$y' - 8 = 3x' - 9$
$3x' - y' = 1$
... (i)
Next, consider the midpoint of the line segment $PQ$. Let $M$ be the midpoint of $PQ$.
The coordinates of the midpoint $M$ are given by $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$.
Coordinates of $M = \left(\frac{3 + x'}{2}, \frac{8 + y'}{2}\right)$
Using midpoint formula
The midpoint $M$ must lie on the mirror line $x + 3y - 7 = 0$. Substitute the coordinates of $M$ into the equation of the line.
$\left(\frac{3 + x'}{2}\right) + 3\left(\frac{8 + y'}{2}\right) - 7 = 0$
Midpoint M satisfies line equation
Multiply the entire equation by 2 to clear the denominators:
$2 \times \left[ \left(\frac{3 + x'}{2}\right) + 3\left(\frac{8 + y'}{2}\right) - 7 \right] = 2 \times 0$
$(3 + x') + 3(8 + y') - 14 = 0$
$3 + x' + 24 + 3y' - 14 = 0$
$x' + 3y' + 13 = 0$
$x' + 3y' = -13$
... (ii)
Now we need to solve the system of two linear equations for $x'$ and $y'$:
$(i) \quad 3x' - y' = 1$
$(ii) \quad x' + 3y' = -13$
From equation (i), we can express $y'$ in terms of $x'$:
$y' = 3x' - 1$
From (i)
Substitute this expression for $y'$ into equation (ii):
$x' + 3(3x' - 1) = -13$
Substitute $y'$ into (ii)
$x' + 9x' - 3 = -13$
$10x' - 3 = -13$
$10x' = -13 + 3$
$10x' = -10$
$x' = -1$
x-coordinate of image Q
Now substitute the value of $x' = -1$ back into the expression for $y'$ ($y' = 3x' - 1$):
$y' = 3(-1) - 1$
Substitute $x'$ value
$y' = -3 - 1$
$y' = -4$
y-coordinate of image Q
Therefore, the coordinates of the image point $Q(x', y')$ are $(-1, -4)$.
Alternate Solution (Using Formula):
The image $(x', y')$ of a point $(x_1, y_1)$ in the line $ax + by + c = 0$ is given by the formula:
$\frac{x' - x_1}{a} = \frac{y' - y_1}{b} = \frac{-2(ax_1 + by_1 + c)}{a^2 + b^2}$
Image formula
Given point $(x_1, y_1) = (3, 8)$ and the line $x + 3y - 7 = 0$, we have $a=1$, $b=3$, and $c=-7$.
Substitute these values into the formula:
$\frac{x' - 3}{1} = \frac{y' - 8}{3} = \frac{-2(1(3) + 3(8) - 7)}{1^2 + 3^2}$
$\frac{x' - 3}{1} = \frac{y' - 8}{3} = \frac{-2(3 + 24 - 7)}{1 + 9}$
$\frac{x' - 3}{1} = \frac{y' - 8}{3} = \frac{-2(20)}{10}$
$\frac{x' - 3}{1} = \frac{y' - 8}{3} = \frac{-40}{10}$
$\frac{x' - 3}{1} = \frac{y' - 8}{3} = -4$
Simplified expression
Equating the first part to $-4$:
$\frac{x' - 3}{1} = -4$
$x' - 3 = -4$
$x' = -4 + 3 = -1$
Equating the second part to $-4$:
$\frac{y' - 8}{3} = -4$
$y' - 8 = -4 \times 3 = -12$
$y' = -12 + 8 = -4$
Using the formula, the image point is $(-1, -4)$, which matches the result obtained using the geometric method.
The image of the point $(3, 8)$ with respect to the line $x + 3y = 7$ is $(-1, -4)$.
Question 19. If the lines y = 3x + 1 and 2y = x + 3 are equally inclined to the line y = mx + 4, find the value of m.
Answer:
Given:
Line 1: $L_1: y = 3x + 1$. Slope $m_1 = 3$.
Line 2: $L_2: 2y = x + 3 \implies y = \frac{1}{2}x + \frac{3}{2}$. Slope $m_2 = \frac{1}{2}$.
Line 3: $L_3: y = mx + 4$. Slope $m_3 = m$.
Lines $L_1$ and $L_2$ are equally inclined to line $L_3$.
To Find:
The value of $m$.
Solution:
If two lines $L_1$ and $L_2$ are equally inclined to a line $L_3$, it means the angle between $L_1$ and $L_3$ is equal to the angle between $L_2$ and $L_3$.
Let $\theta_1$ be the angle between $L_1$ and $L_3$, and $\theta_2$ be the angle between $L_2$ and $L_3$. We are given $\theta_1 = \theta_2$.
The formula for the angle $\alpha$ between two lines with slopes $M_1$ and $M_2$ is $\tan \alpha = \left|\frac{M_2 - M_1}{1 + M_1 M_2}\right|$.
Angle between $L_1$ (slope $m_1 = 3$) and $L_3$ (slope $m_3 = m$):
$\tan \theta_1 = \left|\frac{m - 3}{1 + 3m}\right|$
Tangent of angle between $L_1$ and $L_3$
Angle between $L_2$ (slope $m_2 = \frac{1}{2}$) and $L_3$ (slope $m_3 = m$):
$\tan \theta_2 = \left|\frac{m - \frac{1}{2}}{1 + \frac{1}{2}m}\right|$
Tangent of angle between $L_2$ and $L_3$
$\tan \theta_2 = \left|\frac{\frac{2m - 1}{2}}{\frac{2 + m}{2}}\right| = \left|\frac{2m - 1}{2 + m}\right|$
Since the lines are equally inclined, $\tan \theta_1 = \tan \theta_2$.
$\left|\frac{m - 3}{1 + 3m}\right| = \left|\frac{2m - 1}{2 + m}\right|$
Condition for equal inclination
This implies two possibilities:
Case 1: $\frac{m - 3}{1 + 3m} = \frac{2m - 1}{2 + m}$
Cross-multiply:
$(m - 3)(2 + m) = (2m - 1)(1 + 3m)$
$2m + m^2 - 6 - 3m = 2m + 6m^2 - 1 - 3m$
$m^2 - m - 6 = 6m^2 - m - 1$
Move all terms to one side:
$6m^2 - m^2 - m + m - 1 + 6 = 0$
$5m^2 + 5 = 0$
$5(m^2 + 1) = 0$
This equation has no real solution for $m$ since $m^2 + 1$ is always positive for real $m$.
Case 2: $\frac{m - 3}{1 + 3m} = -\left(\frac{2m - 1}{2 + m}\right) = \frac{1 - 2m}{2 + m}$
Cross-multiply:
$(m - 3)(2 + m) = (1 - 2m)(1 + 3m)$
$m^2 - m - 6 = 1 + 3m - 2m - 6m^2$
$m^2 - m - 6 = 1 + m - 6m^2$
Move all terms to one side:
$m^2 + 6m^2 - m - m - 6 - 1 = 0$
$7m^2 - 2m - 7 = 0$
Quadratic equation for m
This is a quadratic equation in $m$. We can use the quadratic formula $m = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ to solve for $m$, where $a=7$, $b=-2$, and $c=-7$.
$m = \frac{-(-2) \pm \sqrt{(-2)^2 - 4(7)(-7)}}{2(7)}$
$m = \frac{2 \pm \sqrt{4 + 196}}{14}$
$m = \frac{2 \pm \sqrt{200}}{14}$
$m = \frac{2 \pm \sqrt{100 \times 2}}{14}$
$m = \frac{2 \pm 10\sqrt{2}}{14}$
$m = \frac{2(1 \pm 5\sqrt{2})}{14}$
$m = \frac{1 \pm 5\sqrt{2}}{7}$
There are two possible values for $m$ for which the line $y = mx + 4$ is equally inclined to the lines $y = 3x + 1$ and $2y = x + 3$. These values are $\frac{1 + 5\sqrt{2}}{7}$ and $\frac{1 - 5\sqrt{2}}{7}$.
Question 20. If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y + 7 = 0 is always 10. Show that P must move on a line.
Answer:
Given:
A variable point $P(x, y)$.
Line 1 ($L_1$): $x + y - 5 = 0$.
Line 2 ($L_2$): $3x - 2y + 7 = 0$.
The sum of the perpendicular distances from point $P(x, y)$ to lines $L_1$ and $L_2$ is always 10.
To Show:
The path (locus) of the variable point $P(x, y)$ is a straight line.
Solution:
Let $d_1$ be the perpendicular distance from the point $P(x, y)$ to the line $L_1: x + y - 5 = 0$.
Using the distance formula from a point $(x_0, y_0)$ to a line $Ax + By + C = 0$, which is $\frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$:
$d_1 = \frac{|x + y - 5|}{\sqrt{1^2 + 1^2}} = \frac{|x + y - 5|}{\sqrt{2}}$
Distance from P to $L_1$
Let $d_2$ be the perpendicular distance from the point $P(x, y)$ to the line $L_2: 3x - 2y + 7 = 0$.
$d_2 = \frac{|3x - 2y + 7|}{\sqrt{3^2 + (-2)^2}} = \frac{|3x - 2y + 7|}{\sqrt{9 + 4}} = \frac{|3x - 2y + 7|}{\sqrt{13}}$
Distance from P to $L_2$
According to the given condition, the sum of these distances is always 10:
$d_1 + d_2 = 10$
Given condition
$\frac{|x + y - 5|}{\sqrt{2}} + \frac{|3x - 2y + 7|}{\sqrt{13}} = 10$
To remove the absolute value signs, we need to consider the different regions created by the lines $L_1$ and $L_2$. The expression inside an absolute value $|E|$ is either $E$ or $-E$. Thus, there are four possible cases for the equation:
Case 1: $(x + y - 5)$ is non-negative AND $(3x - 2y + 7)$ is non-negative.
$\frac{x + y - 5}{\sqrt{2}} + \frac{3x - 2y + 7}{\sqrt{13}} = 10$
Multiply by $\sqrt{26}$ (LCM of $\sqrt{2}$ and $\sqrt{13}$):
$\sqrt{13}(x + y - 5) + \sqrt{2}(3x - 2y + 7) = 10\sqrt{26}$
$\sqrt{13}x + \sqrt{13}y - 5\sqrt{13} + 3\sqrt{2}x - 2\sqrt{2}y + 7\sqrt{2} = 10\sqrt{26}$
$(\sqrt{13} + 3\sqrt{2})x + (\sqrt{13} - 2\sqrt{2})y - (5\sqrt{13} - 7\sqrt{2} + 10\sqrt{26}) = 0$
This is a linear equation in x and y
Case 2: $(x + y - 5)$ is non-negative AND $(3x - 2y + 7)$ is negative.
$\frac{x + y - 5}{\sqrt{2}} - \frac{3x - 2y + 7}{\sqrt{13}} = 10$
Multiply by $\sqrt{26}$:
$\sqrt{13}(x + y - 5) - \sqrt{2}(3x - 2y + 7) = 10\sqrt{26}$
$\sqrt{13}x + \sqrt{13}y - 5\sqrt{13} - 3\sqrt{2}x + 2\sqrt{2}y - 7\sqrt{2} = 10\sqrt{26}$
$(\sqrt{13} - 3\sqrt{2})x + (\sqrt{13} + 2\sqrt{2})y - (5\sqrt{13} + 7\sqrt{2} + 10\sqrt{26}) = 0$
This is a linear equation in x and y
Case 3: $(x + y - 5)$ is negative AND $(3x - 2y + 7)$ is non-negative.
$-\frac{x + y - 5}{\sqrt{2}} + \frac{3x - 2y + 7}{\sqrt{13}} = 10$
Multiply by $\sqrt{26}$:
$-\sqrt{13}(x + y - 5) + \sqrt{2}(3x - 2y + 7) = 10\sqrt{26}$
$-\sqrt{13}x - \sqrt{13}y + 5\sqrt{13} + 3\sqrt{2}x - 2\sqrt{2}y + 7\sqrt{2} = 10\sqrt{26}$
$(-\sqrt{13} + 3\sqrt{2})x + (-\sqrt{13} - 2\sqrt{2})y + (5\sqrt{13} + 7\sqrt{2} - 10\sqrt{26}) = 0$
This is a linear equation in x and y
Case 4: $(x + y - 5)$ is negative AND $(3x - 2y + 7)$ is negative.
$-\frac{x + y - 5}{\sqrt{2}} - \frac{3x - 2y + 7}{\sqrt{13}} = 10$
Multiply by $\sqrt{26}$:
$-\sqrt{13}(x + y - 5) - \sqrt{2}(3x - 2y + 7) = 10\sqrt{26}$
$-\sqrt{13}x - \sqrt{13}y + 5\sqrt{13} - 3\sqrt{2}x + 2\sqrt{2}y - 7\sqrt{2} = 10\sqrt{26}$
$(-\sqrt{13} - 3\sqrt{2})x + (-\sqrt{13} + 2\sqrt{2})y + (5\sqrt{13} - 7\sqrt{2} - 10\sqrt{26}) = 0$
This is a linear equation in x and y
In each of the four cases, the resulting equation is a linear equation in $x$ and $y$ of the form $Ax + By + C = 0$, where $A$, $B$, and $C$ are constants derived from $\sqrt{13}$, $\sqrt{2}$, and the constant 10.
A linear equation in two variables $x$ and $y$ always represents a straight line in the Cartesian plane, provided that the coefficients of $x$ and $y$ are not both zero. In each of the four cases derived above, the coefficients of $x$ are $(\pm \sqrt{13} \pm 3\sqrt{2})$ and the coefficients of $y$ are $(\pm \sqrt{13} \mp 2\sqrt{2})$. For instance, in Case 1, the coefficients are $(\sqrt{13} + 3\sqrt{2})$ and $(\sqrt{13} - 2\sqrt{2})$. Since $\sqrt{13}$ and $\sqrt{2}$ are irrational and linearly independent over rational numbers, these coefficients cannot simultaneously be zero (unless $\sqrt{13} = 3\sqrt{2}$ and $\sqrt{13} = 2\sqrt{2}$, which is not true). Thus, each case represents a straight line.
The locus of point $P$ is the union of parts of these straight lines, restricted to the regions defined by the signs of $(x + y - 5)$ and $(3x - 2y + 7)$. However, the sum of distances being constant defines a single linear equation in $x$ and $y$ when signs are consistently chosen based on the region the point lies in relative to the given lines. The set of points $(x, y)$ satisfying $\frac{|Ax+By+C|}{\sqrt{A^2+B^2}} + \frac{|A'x+B'y+C'|}{\sqrt{A'^2+B'^2}} = k$ can represent one or more straight lines, specifically parts of the angle bisectors of the given lines.
The condition that the sum of perpendicular distances is constant means that the locus of $P(x, y)$ must be a part of one of the lines given by $\frac{x + y - 5}{\sqrt{2}} \pm \frac{3x - 2y + 7}{\sqrt{13}} = \pm 10$. Each of these equations is linear in $x$ and $y$, representing a straight line.
Therefore, the path of the moving point $P(x, y)$ is a straight line.
Question 21. Find equation of the line which is equidistant from parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
Answer:
Given:
Line 1 ($L_1$): $9x + 6y - 7 = 0$.
Line 2 ($L_2$): $3x + 2y + 6 = 0$.
A required line which is equidistant from $L_1$ and $L_2$.
To Find:
The equation of the line that is equidistant from the two given parallel lines.
Solution:
First, check if the given lines are parallel. Compare the ratios of the coefficients of $x$ and $y$ for the two lines.
For $L_1: 9x + 6y - 7 = 0$, $A_1 = 9$, $B_1 = 6$, $C_1 = -7$.
For $L_2: 3x + 2y + 6 = 0$, $A_2 = 3$, $B_2 = 2$, $C_2 = 6$.
$\frac{A_1}{A_2} = \frac{9}{3} = 3$
$\frac{B_1}{B_2} = \frac{6}{2} = 3$
Since $\frac{A_1}{A_2} = \frac{B_1}{B_2} = 3$, the lines are parallel. They are not the same line because $\frac{C_1}{C_2} = \frac{-7}{6} \neq 3$.
The equation of a line equidistant from two parallel lines $Ax + By + C_1 = 0$ and $Ax + By + C_2 = 0$ is given by $Ax + By + \frac{C_1 + C_2}{2} = 0$.
To use this formula, the equations of the parallel lines must have the same coefficients for $x$ and $y$. Multiply the equation of $L_2$ by 3:
$3 \times (3x + 2y + 6) = 3 \times 0$
Multiply $L_2$ equation by 3
$9x + 6y + 18 = 0$
Equivalent equation for $L_2$
Now we have the two parallel lines in the form $Ax + By + C = 0$ with the same $A$ and $B$ values:
$L_1: 9x + 6y - 7 = 0 \implies A=9, B=6, C_1=-7$
$L_2$ (modified): $9x + 6y + 18 = 0 \implies A=9, B=6, C_2=18$
The equation of the line equidistant from these two lines is:
$9x + 6y + \frac{-7 + 18}{2} = 0$
Using the equidistant formula
$9x + 6y + \frac{11}{2} = 0$
Multiply the equation by 2 to clear the denominator:
$2 \times \left(9x + 6y + \frac{11}{2}\right) = 2 \times 0$
$18x + 12y + 11 = 0$
Equation of the equidistant line
Alternatively, we can find a point on one line, calculate its distance to the other line, and then find a point on the second line and calculate its distance to the first line, ensuring the mid-line property.
A more direct approach is to consider that the equidistant line is the locus of points $(x, y)$ whose distance from $L_1$ equals its distance from $L_2$.
$\frac{|9x + 6y - 7|}{\sqrt{9^2 + 6^2}} = \frac{|3x + 2y + 6|}{\sqrt{3^2 + 2^2}}$
Distances are equal
$\sqrt{9^2 + 6^2} = \sqrt{81 + 36} = \sqrt{117} = \sqrt{9 \times 13} = 3\sqrt{13}$
$\sqrt{3^2 + 2^2} = \sqrt{9 + 4} = \sqrt{13}$
$\frac{|9x + 6y - 7|}{3\sqrt{13}} = \frac{|3x + 2y + 6|}{\sqrt{13}}$
Multiply both sides by $3\sqrt{13}$:
$|9x + 6y - 7| = 3|3x + 2y + 6|$
This gives two possibilities:
Possibility A: $9x + 6y - 7 = 3(3x + 2y + 6)$
$9x + 6y - 7 = 9x + 6y + 18$
$-7 = 18$
This is a false statement, which indicates that this case does not represent the equidistant line. This case would correspond to the lines themselves if they were the same line (which they are not).
Possibility B: $9x + 6y - 7 = -3(3x + 2y + 6)$
$9x + 6y - 7 = -9x - 6y - 18$
Move all terms to one side:
$9x + 9x + 6y + 6y - 7 + 18 = 0$
$18x + 12y + 11 = 0$
Equation of the equidistant line
This method also gives the same equation. The equation of the line equidistant from the parallel lines $9x + 6y - 7 = 0$ and $3x + 2y + 6 = 0$ is $18x + 12y + 11 = 0$.
Question 22. A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3). Find the coordinates of A.
Answer:
Given:
Incident ray passes through $P(1, 2)$.
The ray reflects on the x-axis at point $A$.
The reflected ray passes through $Q(5, 3)$.
To Find:
The coordinates of the point $A$ on the x-axis.
Solution:
Let the point on the x-axis where the reflection occurs be $A(a, 0)$. (Since A is on the x-axis, its y-coordinate is 0).
We use the principle of reflection: the angle of incidence equals the angle of reflection. When a ray reflects off a line, the incident ray, the reflected ray, and the normal to the mirror at the point of incidence are coplanar, and the angle between the incident ray and the normal is equal to the angle between the reflected ray and the normal.
For reflection off the x-axis (which is a horizontal line), the normal is a vertical line. The angles of incidence and reflection are usually measured with respect to the normal or with respect to the mirror itself. If measured with respect to the mirror (the x-axis in this case), the angle the incident ray makes with the x-axis is equal to the angle the reflected ray makes with the x-axis. However, one angle is above the axis, and the other is below, so their slopes will have opposite signs.
Let $P(1, 2)$ be the point on the incident ray and $Q(5, 3)$ be the point on the reflected ray.
Let $A(a, 0)$ be the point of reflection on the x-axis.
The slope of the incident ray $PA$ is $m_{PA} = \frac{0 - 2}{a - 1} = \frac{-2}{a - 1}$.
The slope of the reflected ray $AQ$ is $m_{AQ} = \frac{3 - 0}{5 - a} = \frac{3}{5 - a}$.
According to the laws of reflection, the angle of incidence equals the angle of reflection. If we consider the angles made with the x-axis, the angle the incident ray makes with the positive x-axis and the angle the reflected ray makes with the positive x-axis have a specific relationship.
Let $\theta_1$ be the angle the incident ray $PA$ makes with the positive x-axis, and $\theta_2$ be the angle the reflected ray $AQ$ makes with the positive x-axis. Let $\phi$ be the angle of incidence (between PA and the normal, which is along the y-axis). Let $\psi$ be the angle of reflection (between AQ and the normal).
If the incident ray goes from above the x-axis down towards it (as $P(1, 2)$ has a positive y-coordinate), it makes an angle with the negative direction of the normal (downwards). The reflected ray goes from the x-axis upwards (towards $Q(5, 3)$ which has a positive y-coordinate) and makes an angle with the positive direction of the normal (upwards).
A more direct approach using slopes: If the incident ray has slope $m_{inc}$ and the reflected ray has slope $m_{ref}$ upon reflection from the x-axis, then $m_{ref} = -m_{inc}$.
Here, the ray goes from P to A (incident) and then from A to Q (reflected).
$m_{AQ} = -m_{PA}$
Reflection property off x-axis
Substitute the slopes we calculated:
$\frac{3}{5 - a} = -\left(\frac{-2}{a - 1}\right)$
$\frac{3}{5 - a} = \frac{2}{a - 1}$
Cross-multiply:
$3(a - 1) = 2(5 - a)$
$3a - 3 = 10 - 2a$
Rearrange the terms to solve for $a$:
$3a + 2a = 10 + 3$
$5a = 13$
$a = \frac{13}{5}$
x-coordinate of A
Since the point $A$ is on the x-axis, its y-coordinate is 0.
Therefore, the coordinates of point $A$ are $\left(\frac{13}{5}, 0\right)$.
Alternate Method (Using Image):
The image of a point $(x_1, y_1)$ reflected across the x-axis ($y = 0$) is $(x_1, -y_1)$.
Let $P'(1, -2)$ be the image of the point $P(1, 2)$ reflected across the x-axis.
According to the laws of reflection, the reflected ray appears to come from the image of the source point. This means the reflected ray passes through the point of reflection $A$ and the image point $P'$. Therefore, the points $P'(1, -2)$, $A(a, 0)$, and $Q(5, 3)$ are collinear.
Since the three points are collinear, the slope of $P'A$ must be equal to the slope of $AQ$ (or $P'Q$).
Slope of $P'A$: $m_{P'A} = \frac{0 - (-2)}{a - 1} = \frac{2}{a - 1}$.
Slope of $AQ$: $m_{AQ} = \frac{3 - 0}{5 - a} = \frac{3}{5 - a}$.
Equating the slopes:
$\frac{2}{a - 1} = \frac{3}{5 - a}$
Condition for collinearity
Cross-multiply:
$2(5 - a) = 3(a - 1)$
$10 - 2a = 3a - 3$
$10 + 3 = 3a + 2a$
$13 = 5a$
$a = \frac{13}{5}$
The x-coordinate of point $A$ is $\frac{13}{5}$. Since $A$ is on the x-axis, its y-coordinate is 0.
The coordinates of point $A$ are $\left(\frac{13}{5}, 0\right)$.
Both methods yield the same result. The coordinates of $A$ are $\left(\frac{13}{5}, 0\right)$.
Question 23. Prove that the product of the lengths of the perpendiculars drawn from the points $\left( \sqrt{a^2 - b^2} \;,\; 0 \right)$ and $\left( -\sqrt{a^2 - b^2} \;,\; 0 \right)$ to the line $\frac{x}{a}$ cos θ + $\frac{y}{b}$ sin θ = 1 is b2.
Answer:
Given:
Point 1: $P_1\left( \sqrt{a^2 - b^2} \;,\; 0 \right)$.
Point 2: $P_2\left( -\sqrt{a^2 - b^2} \;,\; 0 \right)$.
Equation of the line: $\frac{x}{a} \cos \theta + \frac{y}{b} \sin \theta = 1$.
We assume $a^2 > b^2$ so that $\sqrt{a^2 - b^2}$ is real.
To Prove:
The product of the lengths of the perpendiculars drawn from $P_1$ and $P_2$ to the given line is $b^2$.
Solution:
The equation of the given line is $\frac{x}{a} \cos \theta + \frac{y}{b} \sin \theta = 1$.
Rewrite the equation in the general form $Ax + By + C = 0$:
$\left(\frac{\cos \theta}{a}\right)x + \left(\frac{\sin \theta}{b}\right)y - 1 = 0$
General form of the line
Here, $A = \frac{\cos \theta}{a}$, $B = \frac{\sin \theta}{b}$, and $C = -1$.
The perpendicular distance from a point $(x_0, y_0)$ to the line $Ax + By + C = 0$ is given by the formula $d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$.
Calculate the denominator $\sqrt{A^2 + B^2}$:
$\sqrt{A^2 + B^2} = \sqrt{\left(\frac{\cos \theta}{a}\right)^2 + \left(\frac{\sin \theta}{b}\right)^2}$
$\sqrt{A^2 + B^2} = \sqrt{\frac{\cos^2 \theta}{a^2} + \frac{\sin^2 \theta}{b^2}}$
$\sqrt{A^2 + B^2} = \sqrt{\frac{b^2 \cos^2 \theta + a^2 \sin^2 \theta}{a^2 b^2}}$
$\sqrt{A^2 + B^2} = \frac{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}{|ab|}$
Denominator for distance formula
Let $d_1$ be the perpendicular distance from $P_1\left( \sqrt{a^2 - b^2} \;,\; 0 \right)$ to the line.
Here $(x_0, y_0) = \left( \sqrt{a^2 - b^2} \;,\; 0 \right)$.
$d_1 = \frac{\left|\left(\frac{\cos \theta}{a}\right)\left(\sqrt{a^2 - b^2}\right) + \left(\frac{\sin \theta}{b}\right)(0) - 1\right|}{\frac{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}{|ab|}}$
$d_1 = \frac{\left|\frac{\cos \theta \sqrt{a^2 - b^2}}{a} - 1\right|}{\frac{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}{|ab|}}$
$d_1 = \frac{\left|\frac{\cos \theta \sqrt{a^2 - b^2} - a}{a}\right|}{\frac{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}{|ab|}}$
$d_1 = \frac{|\cos \theta \sqrt{a^2 - b^2} - a|}{|a|} \times \frac{|ab|}{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}$
$d_1 = \frac{|\cos \theta \sqrt{a^2 - b^2} - a| |b|}{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}$
Distance from $P_1$
Let $d_2$ be the perpendicular distance from $P_2\left( -\sqrt{a^2 - b^2} \;,\; 0 \right)$ to the line.
Here $(x_0, y_0) = \left( -\sqrt{a^2 - b^2} \;,\; 0 \right)$.
$d_2 = \frac{\left|\left(\frac{\cos \theta}{a}\right)\left(-\sqrt{a^2 - b^2}\right) + \left(\frac{\sin \theta}{b}\right)(0) - 1\right|}{\frac{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}{|ab|}}$
$d_2 = \frac{\left|-\frac{\cos \theta \sqrt{a^2 - b^2}}{a} - 1\right|}{\frac{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}{|ab|}}$
$d_2 = \frac{\left|\frac{-\cos \theta \sqrt{a^2 - b^2} - a}{a}\right|}{\frac{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}{|ab|}}$
$d_2 = \frac{|-(\cos \theta \sqrt{a^2 - b^2} + a)|}{|a|} \times \frac{|ab|}{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}$
$d_2 = \frac{|\cos \theta \sqrt{a^2 - b^2} + a| |b|}{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}$
Distance from $P_2$
Now, calculate the product of the lengths of the perpendiculars $d_1 d_2$:
$d_1 d_2 = \frac{|\cos \theta \sqrt{a^2 - b^2} - a| |b|}{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}} \times \frac{|\cos \theta \sqrt{a^2 - b^2} + a| |b|}{\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta}}$
$d_1 d_2 = \frac{|(\cos \theta \sqrt{a^2 - b^2} - a)(\cos \theta \sqrt{a^2 - b^2} + a)| |b|^2}{(\sqrt{b^2 \cos^2 \theta + a^2 \sin^2 \theta})^2}$
Use the difference of squares formula $(X - Y)(X + Y) = X^2 - Y^2$ in the numerator inside the absolute value, where $X = \cos \theta \sqrt{a^2 - b^2}$ and $Y = a$. Also, $|b|^2 = b^2$ and $(\sqrt{E})^2 = E$ for $E \ge 0$.
$d_1 d_2 = \frac{|(\cos \theta \sqrt{a^2 - b^2})^2 - a^2| b^2}{b^2 \cos^2 \theta + a^2 \sin^2 \theta}$
$d_1 d_2 = \frac{|\cos^2 \theta (a^2 - b^2) - a^2| b^2}{b^2 \cos^2 \theta + a^2 \sin^2 \theta}$
$d_1 d_2 = \frac{|a^2 \cos^2 \theta - b^2 \cos^2 \theta - a^2| b^2}{b^2 \cos^2 \theta + a^2 \sin^2 \theta}$
$d_1 d_2 = \frac{|a^2 (\cos^2 \theta - 1) - b^2 \cos^2 \theta| b^2}{b^2 \cos^2 \theta + a^2 \sin^2 \theta}$
Using the identity $\cos^2 \theta - 1 = -\sin^2 \theta$:
$d_1 d_2 = \frac{|a^2 (-\sin^2 \theta) - b^2 \cos^2 \theta| b^2}{b^2 \cos^2 \theta + a^2 \sin^2 \theta}$
$d_1 d_2 = \frac{|-a^2 \sin^2 \theta - b^2 \cos^2 \theta| b^2}{b^2 \cos^2 \theta + a^2 \sin^2 \theta}$
$d_1 d_2 = \frac{|-(a^2 \sin^2 \theta + b^2 \cos^2 \theta)| b^2}{b^2 \cos^2 \theta + a^2 \sin^2 \theta}$
Since $a^2 \sin^2 \theta + b^2 \cos^2 \theta \ge 0$, $|-(a^2 \sin^2 \theta + b^2 \cos^2 \theta)| = a^2 \sin^2 \theta + b^2 \cos^2 \theta$.
$d_1 d_2 = \frac{(a^2 \sin^2 \theta + b^2 \cos^2 \theta) b^2}{b^2 \cos^2 \theta + a^2 \sin^2 \theta}$
$d_1 d_2 = \frac{(b^2 \cos^2 \theta + a^2 \sin^2 \theta) b^2}{b^2 \cos^2 \theta + a^2 \sin^2 \theta}$
Cancel the common term in the numerator and denominator (assuming it's not zero):
$d_1 d_2 = b^2$
The points $\left( \sqrt{a^2 - b^2} \;,\; 0 \right)$ and $\left( -\sqrt{a^2 - b^2} \;,\; 0 \right)$ are the foci of an ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ (assuming $a^2 > b^2$). The given line is a tangent to this ellipse. The product of the perpendiculars from the foci to any tangent of an ellipse is equal to the square of the semi-minor axis ($b^2$). The proof confirms this geometric property.
Question 24. A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow.
Answer:
Given:
Equation of the first path: $L_1: 2x - 3y + 4 = 0$.
Equation of the second path: $L_2: 3x + 4y - 5 = 0$.
Equation of the target path: $L_3: 6x - 7y + 8 = 0$.
The person starts at the junction of $L_1$ and $L_2$ and wants to reach $L_3$ in the least time.
To Find:
The equation of the path the person should follow.
Solution:
The person is standing at the point of intersection of lines $L_1$ and $L_2$. To find this point, we solve the system of equations:
$2x - 3y = -4$
... (i)
$3x + 4y = 5$
... (ii)
Multiply equation (i) by 4 and equation (ii) by 3 to eliminate $y$:
$4 \times (2x - 3y) = 4 \times (-4) \implies 8x - 12y = -16$
Multiply (i) by 4
$3 \times (3x + 4y) = 3 \times 5 \implies 9x + 12y = 15$
Multiply (ii) by 3
Add the new equations:
$(8x - 12y) + (9x + 12y) = -16 + 15$
$17x = -1$
$x = -\frac{1}{17}$
x-coordinate of intersection
Substitute the value of $x = -\frac{1}{17}$ into equation (i) to find $y$:
$2\left(-\frac{1}{17}\right) - 3y + 4 = 0$
Substitute x into (i)
$-\frac{2}{17} - 3y + 4 = 0$
$-3y = \frac{2}{17} - 4 = \frac{2 - 68}{17}$
$-3y = -\frac{66}{17}$
$y = \frac{66}{17 \times 3} = \frac{22}{17}$
y-coordinate of intersection
The starting point of the person is $P\left(-\frac{1}{17}, \frac{22}{17}\right)$.
To reach the target path $L_3$ in the least time, the person should follow the path that is perpendicular to $L_3$ and passes through the starting point $P$.
Find the slope of the target line $L_3: 6x - 7y + 8 = 0$. Rewrite the equation in slope-intercept form $y = mx + c$:
$-7y = -6x - 8$
$y = \frac{-6x - 8}{-7} = \frac{6}{7}x + \frac{8}{7}$
Slope-intercept form of $L_3$
The slope of the target line $L_3$ is $m_3 = \frac{6}{7}$.
Let $m_p$ be the slope of the required path (the perpendicular line). Since the path is perpendicular to $L_3$, the product of their slopes is $-1$:
$m_p \times m_3 = -1$
Perpendicular slopes condition
$m_p \times \frac{6}{7} = -1$
$m_p = -\frac{7}{6}$
Slope of the required path
Now, we find the equation of the line that passes through the point $P\left(-\frac{1}{17}, \frac{22}{17}\right)$ and has a slope $m_p = -\frac{7}{6}$. Using the point-slope form $y - y_1 = m(x - x_1)$:
$y - \frac{22}{17} = -\frac{7}{6}\left(x - \left(-\frac{1}{17}\right)\right)$
Point-slope form
$y - \frac{22}{17} = -\frac{7}{6}\left(x + \frac{1}{17}\right)$
To clear the denominators, multiply both sides by the LCM of 17 and 6, which is $17 \times 6 = 102$:
$102\left(y - \frac{22}{17}\right) = 102\left(-\frac{7}{6}\right)\left(x + \frac{1}{17}\right)$
$102y - 102 \times \frac{22}{17} = -17 \times 7 \left(x + \frac{1}{17}\right)$
$102y - 6 \times 22 = -119x - 119 \times \frac{1}{17}$
$102y - 132 = -119x - 7$
Rearrange the equation to the general form $Ax + By + C = 0$:
$119x + 102y - 132 + 7 = 0$
$119x + 102y - 125 = 0$
Equation of the path to follow
The equation of the path that the person should follow to reach the line $6x - 7y + 8 = 0$ in the least time is $119x + 102y - 125 = 0$.

